题目内容
14. 如图,在直角三角形纸片ABC中,AC=8,BC=6.现将△ABC按如图方式折叠,使点A与点B重合,折痕为DE,求sin∠CBE的值.
如图,在直角三角形纸片ABC中,AC=8,BC=6.现将△ABC按如图方式折叠,使点A与点B重合,折痕为DE,求sin∠CBE的值.
分析 先根据图形翻折变换的性质得出BE=AE,设CE=x,则BE=AE=8-x,根据勾股定理求出x的值,再由锐角三角函数的定义即可得出结论.
解答 解:∵△BDE由△ADE翻折而成,
∴BE=AE.
设CE=x,则BE=AE=8-x,
在Rt△BCE中,BC2+CE2=BE2,即62+x2=(8-x)2,
解得x=$\frac{7}{4}$,
∴tan∠CBE=$\frac{CE}{AC}$=$\frac{7}{24}$.
点评 本题考查的是翻折变换,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
19.若α是锐角,且cosα=tan30°,则( )
| A. | 0°<α<30° | B. | 30°≤α<45° | C. | 45°<α<60° | D. | 60°≤α<90° |
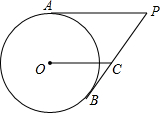 如图,PA,PB分别与⊙O相切于点A,B,OC∥AP交PB于C.
如图,PA,PB分别与⊙O相切于点A,B,OC∥AP交PB于C.