题目内容
11.如图由“?”拼出的一列形如正方形的图案,每条边上(包括两个顶点)有n(n>1)个“?”,每个图形“?”的总数是S: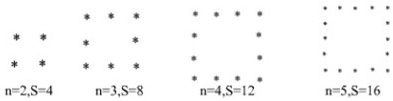
通过观察规律可以推断出:当n=8时,S=28.
分析 根据正方形周长的求解方法可知:每条边有n个“?”,可得共有4n,再注意每个顶点上的点重复数了一次,所以每个图案“?”的总数还要去掉4个,即得每条边有(n-1)个“?”(n>1),每个图案花盆的总数是s=4n-4,据此可得.
解答 解:∵当n=2时,S=2×4-4=4,
当n=3时,S=3×4-4=8,
当n=4时,S=4×4-4=12,
当n=5时,S=5×4-4=16,
…
∴当n=8时,S=8×4-4=28,
故答案为:28.
点评 此题考查了图形的变化类;根据所给图形判断出“?”的总数与边数之间的关系式是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.若α是锐角,且cosα=tan30°,则( )
| A. | 0°<α<30° | B. | 30°≤α<45° | C. | 45°<α<60° | D. | 60°≤α<90° |
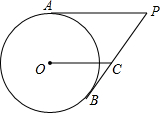 如图,PA,PB分别与⊙O相切于点A,B,OC∥AP交PB于C.
如图,PA,PB分别与⊙O相切于点A,B,OC∥AP交PB于C. 当测量底部不可以直接到达的物体的高度.
当测量底部不可以直接到达的物体的高度.