题目内容
20. 如图,在四边形ABCD中,∠B=∠D=90°,AE平分∠BAD交CD于点E,CF平分∠BCD交AB于点F,求证:AE∥CF.
如图,在四边形ABCD中,∠B=∠D=90°,AE平分∠BAD交CD于点E,CF平分∠BCD交AB于点F,求证:AE∥CF.
分析 根据∠BAD与∠BCD互补,得出∠EA与∠FCB互余,根据∠B=90°,得出∠CFB与∠FCB互余,进而得到∠CFB=∠EAB,并得出结论.
解答  证明:∵∠B=∠D=90°,
证明:∵∠B=∠D=90°,
∴∠DAB+∠DCB=180°,∠CFB+∠FCB=90°,
∵AE平分∠BAD交CD于点E,CF平分∠BCD交AB于点F,
∴∠EAB+∠FCB=$\frac{1}{2}$∠DAB+$\frac{1}{2}$∠DCB=90°,
∴∠CFB=∠EAB,
∴AE∥CF.
点评 本题主要考查了平行线的判定,两条直线被第三条所截,如果同位角相等,那么这两条直线平行. 即同位角相等,两直线平行.根据同角的余角相等进行推导是证明的主要依据.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
8.两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
(1)求得样本容量为50,并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.

| 发言次数n | |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.
5.下列各组数中,可以构成勾股数的是( )
| A. | 13,16,19 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 18,24,36 | D. | 12,35,37 |
 如图,△ABC的三个顶点分别为A(1,1)、B(4,2)、C(3,4).
如图,△ABC的三个顶点分别为A(1,1)、B(4,2)、C(3,4). 如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.
如图,已知BC∥DE,∠ABC=120°,那么直线AB、DE的夹角是120°或60°.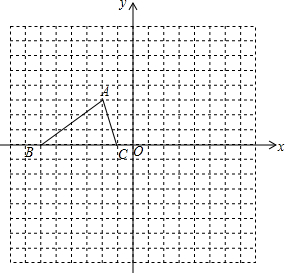 如图,已知△ABC的三个顶点坐标为A(-2,3),B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点坐标为A(-2,3),B(-6,0),C(-1,0).