题目内容
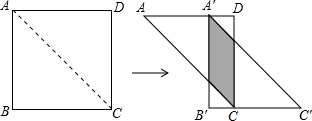
如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 .

考点:平移的性质,解一元二次方程-因式分解法,平行四边形的判定与性质,正方形的性质
专题:几何动点问题
分析:根据平移的性质,结合阴影部分是平行四边形,△AA′H与△HCB′都是等腰直角三角形,则若设AA′=x,则阴影部分的底长为x,高A′D=12-x,根据平行四边形的面积公式即可列出方程求解.
解答: 解:设AC交A′B′于H,
解:设AC交A′B′于H,
∵∠A=45°,∠D=90°
∴△A′HA是等腰直角三角形
设AA′=x,则阴影部分的底长为x,高A′D=12-x
∴x•(12-x)=32
∴x=4或8,
即AA′=4或8cm.
故答案为:4或8.
 解:设AC交A′B′于H,
解:设AC交A′B′于H,∵∠A=45°,∠D=90°
∴△A′HA是等腰直角三角形
设AA′=x,则阴影部分的底长为x,高A′D=12-x
∴x•(12-x)=32
∴x=4或8,
即AA′=4或8cm.
故答案为:4或8.
点评:考查了平移的性质及一元二次方程的解法等知识,解决本题关键是抓住平移后图形的特点,利用方程方法解题.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
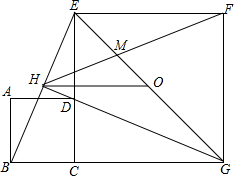 如图,正方形ABCD的边CD与正方形CGFE的边CE重合,O是EG的中点,∠EGC的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:
如图,正方形ABCD的边CD与正方形CGFE的边CE重合,O是EG的中点,∠EGC的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:①GH⊥BE;②HO
| ∥ |
. |
| 1 |
| 2 |
其中正确的结论有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
不等式组2≤3x-7<9的所有整数解为( )
| A、3,4 | B、4,5 |
| C、3,4,5 | D、3,4,5,6 |
 某校为了了解九年级男生立定跳远的成绩,从该校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
某校为了了解九年级男生立定跳远的成绩,从该校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表: 如图,在矩形ABCD中,AD=9cm,AB=3cm,将其折叠,使点D和点B重合,则重叠部分(△BEF)的面积为
如图,在矩形ABCD中,AD=9cm,AB=3cm,将其折叠,使点D和点B重合,则重叠部分(△BEF)的面积为