题目内容
如图，已知等边三角形ABC的边长为2a，求其内切圆的内接正方形DEFG的周长和面积．考点：三角形的内切圆与内心
专题：
分析：利用正三角形的性质以及其内切圆的性质得出圆的半径，再利用正方形的性质得出其边长，进而得出答案．
解答：
解：如图所示：连接CO，OD，OE，设N为切点，连接ON，
∵等边三角形ABC的边长为2a，
∴NC=a，∠OCN=30°，
则NO=atan30°=
a，
故DO=EO=
a，
则DE=
a×
=
a，
故内切圆的内接正方形DEFG的周长为：
a×4=
a；
其面积为：（
a）2=
a2．
解：如图所示：连接CO，OD，OE，设N为切点，连接ON，∵等边三角形ABC的边长为2a，
∴NC=a，∠OCN=30°，
则NO=atan30°=
| ||
| 3 |
故DO=EO=
| ||
| 3 |
则DE=
| ||
| 3 |
| 2 |
| ||
| 3 |
故内切圆的内接正方形DEFG的周长为：
| ||
| 3 |
4
| ||
| 3 |
其面积为：（
| ||
| 3 |
| 2 |
| 3 |
点评：此题主要考查了正三角形和正方形的性质，得出内切圆半径的长是解题关键．
练习册系列答案
相关题目
如图，长方形OABC在平面直角坐标系xOy的第一象限内，点A在x轴正半轴上，点C在y轴的正半轴上，点D、E分别是OC、BC的中点，∠CDE=30°，点E的坐标为（2，a）．下列说法正确的是（ ）
| A、球的截面可能是椭圆 |
| B、组成长方体的各个面中不能有正方形 |
| C、五棱柱一共有15条棱 |
| D、正方体的截面可能是七边形 |
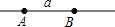如图，下列说法正确的是（ ）| A、直线AB和直线a不是同一条直线 |
| B、直线AB和直线BA是两条直线 |
| C、射线AB和射线BA是两条射线 |
| D、线段AB和线段BA是两条线段 |
