题目内容
18.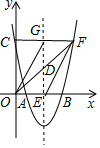 如图,过点F(6,5)的抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C.且B(5,0)
如图,过点F(6,5)的抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C.且B(5,0)(1)求此抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,交CF于点G,连接OG、EF,试判断四边形OEFG的形状,并说明理由;
(3)在(2)的条件下,连接OF交对称轴于点D,抛物线对称轴上是否存在点P,使△OFP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)把点F(6,5)、B(5,0)代入抛物线求出b和c的值即可;
(2)求出C(0,5),得出CF∥OE,证出GF=AE=3,即可得出四边形OEFG为平行四边形;
(3)求出D(3,2.5),分情况讨论:①当点O为直角顶点时,证明△OED∽△PEO,得出$\frac{OE}{PE}=\frac{DE}{OE}$,求出PE=$\frac{18}{5}$,即可得出P的坐标;
②当点F为直角顶点时,同理可得FG2=PG•GD,求出PG=$\frac{18}{5}$,得出PE=$\frac{43}{5}$,即可得出P的坐标;
③当点P为直角顶点时,由勾股定理得OF=$\sqrt{61}$,由直角三角形斜边上的中线性质得出PD=$\frac{\sqrt{61}}{2}$,若点P在OD上方,则PE=$\frac{\sqrt{61}+5}{2}$,得出P(3,$\frac{\sqrt{61}+5}{2}$);
若点P在OD下方时,则PE=$\frac{\sqrt{61}-5}{2}$,得出P(3,-$\frac{\sqrt{61}-5}{2}$);即可得出结论.
解答 解:(1)∵抛物线过点F(6,5)、B(5,0),
∴$\left\{\begin{array}{l}{36+6b+c=5}\\{25+5b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-6}\\{c=5}\end{array}\right.$,
∴此抛物线的解析式为:y=x2-6x+5;
(2)四边形OEFG为平行四边形.
∵此抛物线与y轴交于点C,
∴C(0,5),
又∵F(6,5),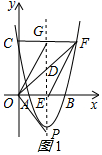
∴CF∥OE,
又∵抛物线的对称轴为:x=3,
∴G(3,5),E(3,0),
∴GF=AE=3,
∴四边形OEFG为平行四边形;
(3)∵F(6,5),
∴D(3,2.5),
①当点O为直角顶点时,如图1所示: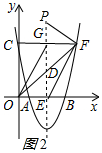
则∠POF=90°=∠OED,
∴∠POE=∠ODE,
∴△OED∽△PEO,
∴$\frac{OE}{PE}=\frac{DE}{OE}$,即$\frac{3}{PE}=\frac{\frac{5}{2}}{3}$,
解得:PE=$\frac{18}{5}$,
∴P(3,-$\frac{18}{5}$),
②当点F为直角顶点时,如图2所示: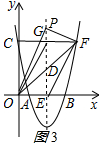
同理可得FG2=PG•GD,
∴PG=$\frac{18}{5}$,
∴PE=$\frac{43}{5}$,
∴P(3,$\frac{43}{5}$);
③当点P为直角顶点时,由勾股定理得OF=$\sqrt{{6}^{2}+{5}^{2}}$=$\sqrt{61}$,
又∵PD是Rt△OPF斜边OF上的中线,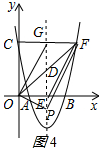
∴PD=$\frac{\sqrt{61}}{2}$,
若点P在OD上方,如图3所示:
则PE=$\frac{\sqrt{61}+5}{2}$,
∴P(3,$\frac{\sqrt{61}+5}{2}$);
若点P在OD下方时,如图4所示:
则PE=$\frac{\sqrt{61}-5}{2}$,
∴P(3,-$\frac{\sqrt{61}-5}{2}$);
综上所述,抛物线的对称轴上存在点P(3,-$\frac{18}{5}$)或(3,$\frac{43}{5}$)或(3,$\frac{\sqrt{61}+5}{2}$)或(3,-$\frac{\sqrt{61}-5}{2}$),使△OFP是直角三角形.
点评 本题是二次函数综合题目,考查了待定系数法求二次函数的解析式、坐标与图形性质、平行四边形的判定、相似三角形的判定与性质、直角三角形的性质、勾股定理等知识;本题综合性强,有一定难度,特别是(3)中,需要进行分类讨论才能得出结论.

 科学实验活动册系列答案
科学实验活动册系列答案
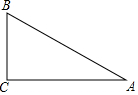 如图,坡面AB的长为40米,坡面的铅垂高度BC为20米.求坡面的坡度和坡角α的度数.
如图,坡面AB的长为40米,坡面的铅垂高度BC为20米.求坡面的坡度和坡角α的度数.