题目内容
6.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.(1)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,则∠ACB=96°.
(2)如图,在△ABC中,AC=2,BC=$\sqrt{2}$,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.

分析 (1)根据相似三角形的性质得到∠BCD=∠A=48°,再根据角的和差关系求出∠ACB即可.
(2)设BD=x,利用△BCD∽△BAC,得$\frac{BC}{BA}$=$\frac{BD}{BC}$,列出方程即可解决问题.
解答  解:(1)当AD=CD时,如图3,∠ACD=∠A=48°,
解:(1)当AD=CD时,如图3,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
(2)由已知AC=AD=2,
∵△BCD∽△BAC,
∴$\frac{BC}{BA}$=$\frac{BD}{BC}$,设BD=x,
∴($\sqrt{2}$)2=x(x+2),
∵x>0,
∴x=$\sqrt{3}$-1,
∵△BCD∽△BAC,
∴$\frac{CD}{AC}$=$\frac{BD}{BC}$=$\frac{\sqrt{3}-1}{\sqrt{2}}$,
∴CD=$\frac{\sqrt{3}-1}{\sqrt{2}}$×2=$\sqrt{6}$-$\sqrt{2}$.
故答案为:96.
点评 本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是理解题意,属于中考常考题型.

练习册系列答案
相关题目
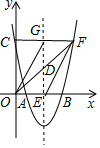 如图,过点F(6,5)的抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C.且B(5,0)
如图,过点F(6,5)的抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C.且B(5,0)