题目内容
20．已知：在△ABC中，∠C=90°，CD是斜边AB上的高，求证：△ACD∽△CBD∽△ABC．分析 利用高的定义得到∠ADC=∠BDC=90°，则根据有两组角对应相等的两个三角形相似可判断△ACD∽△ABC，同理可得△CBD∽△ABC，于是得到△ACD∽△CBD∽△ABC．
解答 解：如图，
∵CD是斜边AB上的高，
∴∠ADC=∠BDC=90°，
∵∠CAD=∠BAC，∠ADC=∠ACB，
∴△ACD∽△ABC，
∵∠BCD=∠BAC，∠CDB=∠ACB，
∴△CBD∽△ABC，
∴△ACD∽△CBD∽△ABC．
点评 本题考查了相似三角形的判断：有两组角对应相等的两个三角形相似．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
如图，已知CD⊥AB，BE⊥AC，证明：$\frac{AB}{AE}$=$\frac{AC}{AD}$．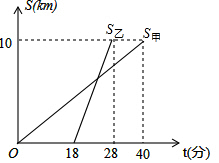
甲、乙两位教师先后从学校出发，到距学校10千米的培训中心参加新教材培训学习，图中S甲、S乙分别表示甲、乙两位教师从学校到培训中心所走的路程s（千米）随时间t（分钟）变化的函数图象．求乙出发后追上甲所用的时间是多少？
如图，G是△ABC的重心，延长AD，使得DH=GD，K为BG中点．求证：△FKG∽△GHC．
5．下列各选项中所叙述的两个三角形中不一定相似的是（ ）
| A． | 各有一个角等于45°的两个等腰三角形 | |
| B． | 各有一个角等于60°的两个等腰三角形 | |
| C． | 两个等腰直角三角形 | |
| D． | 各有一个角等于105°的两个等腰三角形 |
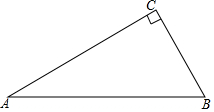如图，△ABC中，∠C=90°，∠A=30°．