题目内容
4.某学校为了表彰进步学生,需要购进一批文具套装作为奖品,套装内包含一个笔盒和一支笔,A和B两个商店均以同样的价格出售同样的笔盒和笔,笔盒每个20元,笔每支5元,但是在A商店购买超过100套装以后,再购买一笔盒就送一支笔,在B商店购买超过150套装以后,超出的套装打六折.(1)若该团要购买180套套装,则在A商店需付4100元,在B商店需付4200元.
(2)请你根据购买量的多少,帮助学校确定到哪家商店来购买该奖品?
分析 (1)根据题意列出解析式,把x=180代入解答即可;
(2)根据两种解析式列出不等式,进而比较即可.
解答 解:(1)根据题意得出需付的费用y和购买的套装数量x之间的函数关系为:
到甲商店购买:y=20x+100×5=20x+500;
到乙商店购买:y=150×25+(x-150)×25×0.6=15x+1500;
该团要购买180套套装,则在A商店需付的钱数是:180×20+500=4100元;
该团要购买180套套装,则在B商店需付的钱数是:15×180+1500=4200元.
故答案为4100,4200;
(2)若20x+500>15x+1500,
解得x>200,
若20x+500=15x+1500,
则x=200,
若20x+500<15x+1500,
则x<200.
所以,若购买量超过200时,到B商店来购买奖品省钱,购买量等于200时,到A、B商店来购买奖品一样,购买量低于200时,到A商店来购买奖品省钱.
点评 本题考查了二元一次方程组和一元一次不等式组的应用,解答本题的关键是读懂题意,找出合适的不等关系,列方程和不等式求解.

练习册系列答案
相关题目
14. 如图,已知:AO⊥BO,CO⊥DO,∠AOD=120°,则∠BOC的度数是( )
如图,已知:AO⊥BO,CO⊥DO,∠AOD=120°,则∠BOC的度数是( )
 如图,已知:AO⊥BO,CO⊥DO,∠AOD=120°,则∠BOC的度数是( )
如图,已知:AO⊥BO,CO⊥DO,∠AOD=120°,则∠BOC的度数是( )| A. | 60° | B. | 80° | C. | 100° | D. | 120° |
 如图,点E,F分别在矩形ABCD的边BC,AD上,EF∥AB,AB=6,AD=8,当AF=$\frac{9}{2}$时,矩形ABEF与矩形ADCB相似.
如图,点E,F分别在矩形ABCD的边BC,AD上,EF∥AB,AB=6,AD=8,当AF=$\frac{9}{2}$时,矩形ABEF与矩形ADCB相似.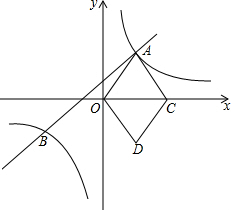 如图,在平面直角坐标系xOy中,直线y=mx+n与双曲线y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点B(-3,-2),D(2,-3),连结OA、OD、DC、AC,四边形AODC为菱形.
如图,在平面直角坐标系xOy中,直线y=mx+n与双曲线y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点B(-3,-2),D(2,-3),连结OA、OD、DC、AC,四边形AODC为菱形.