题目内容
16.已知菱形ABCD的周长是200cm,一条对角线长为60cm,则另一条对角线的长度为80cm.分析 根据菱形的性质求出OA=OC,OB=OD,AC⊥BD,AB=BC=CD=AD,求出AB长,在△AOB中由勾股定理求出OB,即可求出BD.
解答 解:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=$\frac{1}{4}$×200cm=50cm,
AC⊥BD,OA=OC=$\frac{1}{2}$AC=30cm,
在△AOB中,由勾股定理得:OB=$\sqrt{A{B}^{2}-O{A}^{2}}=\sqrt{5{0}^{2}-3{0}^{2}}$=40(cm),
∴BD=2OB=80cm,
故答案为:80cm
点评 本题考查了对菱形的性质和勾股定理的应用,关键是求出OA和AB的长,主要培养了学生运用定理进行计算的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.如果二次函数y=(m-1)x2+2x+1与x轴有两个不同的交点,那么m的取值范围是( )
| A. | m>2 | B. | m<2 | C. | m>2且m≠1 | D. | m<2且m≠1 |
6.为了保护水资源,盐城市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
(1)若某用户六月份用水量为20吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 1.5 |
| 大于10吨不大于m吨部分(10≤m≤50) | 2 |
| 大于m吨部分 | 3 |
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
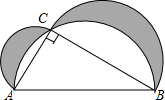 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,分别以AC、BC、AB为直径作半圆,求图中阴影部分的面积.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,分别以AC、BC、AB为直径作半圆,求图中阴影部分的面积.