题目内容
18．
如图，AB∥CD，AB与EC交于点F，如果EA=EF，∠C=110°，则∠E=40度．
分析 先根据平行线的性质求出∠BFC的度数，再由对顶角的性质求出∠AFE的度数，根据EA=EF可得出∠A的度数，由三角形内角和定理即可得出结论．
解答 解：∵AB∥CD，∠C=110°，
∴∠BFC=180°-110°=70°．
∵∠BFC与∠AFE是对顶角，
∴∠AFE=70°．
∵EA=EF，
∴∠A=∠AFE=70°，
∴∠E=180°-∠A-∠AFE=180°-70°-70°=40°．
故答案为：40．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．
练习册系列答案
相关题目
9．在-1，0，2，$\sqrt{3}$四个数中，最大的数是（ ）
| A． | -1 | B． | 0 | C． | 2 | D． | $\sqrt{3}$ |
13．
如图，直线a∥b．若∠1=30°，∠2=45°，则∠3的大小为（ ）
如图，直线a∥b．若∠1=30°，∠2=45°，则∠3的大小为（ ）| A． | 75° | B． | 80° | C． | 85° | D． | 105° |
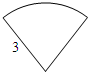如图，半径为3cm的扇形纸片的周长为10cm，将它围成一个圆锥的侧面，则圆锥的底面圆的半径等于$\frac{2}{π}$cm．（结果保留π）
10．
如图，△ABC内接于⊙O，若∠AOB=100°，则∠ACB的度数是（ ）
如图，△ABC内接于⊙O，若∠AOB=100°，则∠ACB的度数是（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 80° |
如图，在△ABC中，AB=AC=10，点D是边BC上一动点（不与B，C重合），∠ADE=∠B=α，DE交AC于点E，且cosα=$\frac{4}{5}$．当BD=6时，△ABD与△DCE全等．
8．
如图所示，AB∥CD，AD与BC相交于点E，EF是∠BED的平分线，若∠1=30°，∠2=40°，则∠BEF=（ ）
如图所示，AB∥CD，AD与BC相交于点E，EF是∠BED的平分线，若∠1=30°，∠2=40°，则∠BEF=（ ）| A． | 70° | B． | 40° | C． | 35° | D． | 30° |