题目内容
20.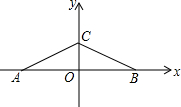 如图,在直角坐标系中,有点A(-2,0)、B(2,0)、C(0,1),另有一点D与点A、B、C构成平行四边形的顶点,则点D的坐标是(4,1),(-4,1),(0,-1).
如图,在直角坐标系中,有点A(-2,0)、B(2,0)、C(0,1),另有一点D与点A、B、C构成平行四边形的顶点,则点D的坐标是(4,1),(-4,1),(0,-1).
分析 根据平行四边形的判定,分别从AC,BC,AB为对角线,去分析求解即可求得答案.
解答  解:①当AB∥CD,且AB=CD时,若以BC为对角线,则四边形ABDC是平行四边形,
解:①当AB∥CD,且AB=CD时,若以BC为对角线,则四边形ABDC是平行四边形,
∵CD=AB=4,
∴点D1的坐标为(4,1);
②当AB∥CD,且AB=CD时,若以AC为对角线,则四边形ABDC是平行四边形,
∵CD=AB=4,
∴点D2的坐标为(-4,1);
③当AB与CD互相平分时,若以AB为对角线,则四边形ADBC是平行四边形,
∵AB与CD的中点重合,
∴点D3的坐标为(0,-1),
综上所述,符合条件的点D的坐标有:(4,1),(-4,1),(0,-1).
故答案为:(4,1),(-4,1),(0,-1).
点评 此题考查了平行四边形的判定,坐标与图形性质.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
相关题目
 已知;如图,AD是△ABC的BC边上的中线,E为AD的中点,连接BE并延长交AC于点F.求EF:BF.
已知;如图,AD是△ABC的BC边上的中线,E为AD的中点,连接BE并延长交AC于点F.求EF:BF. 如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4,求:
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4,求: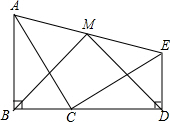 如图,△ABC≌△CDE,B、C、D三点共线,连接AE,点M为AE中点,连接BM、DM,试判断△BMD的形状.
如图,△ABC≌△CDE,B、C、D三点共线,连接AE,点M为AE中点,连接BM、DM,试判断△BMD的形状.

 (1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点,求线段MN的长度;
(1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点,求线段MN的长度;