题目内容
5.传说在19世纪初,一位将军率领部队在一河边与敌军激战,为使炮弹准确落到河对岸的敌军阵地,将军站在河岸边,将帽子压低,使视线沿着帽檐恰好落到河对岸的边线上(如图甲),然后他一步步向后退(如图乙),这时他后退的距离便是河的宽度,为什么?请说明道理.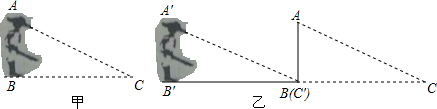
分析 根据将军的身高不变可得AB=A′B′,视线方向不变可得∠A=∠A′,然后利用“角边角”证明△ABC和△A′B′C′全等,根据全等三角形对应边相等可得BC=B′C′,从而得到他后退的距离便是河的宽度.
解答 证明:易知AB=A′B′,∠A=∠A′,
又∵AB⊥BC,A′B′⊥B′C′,
∴∠ABC=∠A′B′C′=90°,
∵在△ABC和△A′B′C′中,
$\left\{\begin{array}{l}{∠A=∠A′}\\{AB=A′B′}\\{∠ABC=∠A′B′C′}\end{array}\right.$,
∴△ABC≌△A′B′C′(ASA),
∴BC=B′C′,
因此,他后退的距离便是河的宽度.
点评 本题考查了全等三角形的应用,根据题目信息,找出三角形全等的条件是解题的关键.

练习册系列答案
相关题目
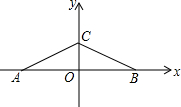 如图,在直角坐标系中,有点A(-2,0)、B(2,0)、C(0,1),另有一点D与点A、B、C构成平行四边形的顶点,则点D的坐标是(4,1),(-4,1),(0,-1).
如图,在直角坐标系中,有点A(-2,0)、B(2,0)、C(0,1),另有一点D与点A、B、C构成平行四边形的顶点,则点D的坐标是(4,1),(-4,1),(0,-1). 已知直线y=3x+3与x轴交于点A,与y轴交于点D,与直线y=$\frac{3}{4}$x交于点E.过点D作DC∥x轴,交直线y=$\frac{3}{4}$x于点C,过点C作CB∥AD交x轴于点B.点P从点O出发,沿线段OC向终点C运动,点Q从点C出发,沿线段CD向终点D运动.若P、Q同时出发,速度均为1单位长度/s,时间为t s.当P、Q两点有一点到达终点时,它们均停止运动.将线段PQ绕点P沿顺时针方向旋转90°.当点Q落在四边形ABCD一边所在的直线上时,t的值为2.
已知直线y=3x+3与x轴交于点A,与y轴交于点D,与直线y=$\frac{3}{4}$x交于点E.过点D作DC∥x轴,交直线y=$\frac{3}{4}$x于点C,过点C作CB∥AD交x轴于点B.点P从点O出发,沿线段OC向终点C运动,点Q从点C出发,沿线段CD向终点D运动.若P、Q同时出发,速度均为1单位长度/s,时间为t s.当P、Q两点有一点到达终点时,它们均停止运动.将线段PQ绕点P沿顺时针方向旋转90°.当点Q落在四边形ABCD一边所在的直线上时,t的值为2. 在△ABC中,BA=BC,D是AC的中点.求证:BD⊥AC.
在△ABC中,BA=BC,D是AC的中点.求证:BD⊥AC. 如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数
如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数 ,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.
,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.