题目内容
10．
已知；如图，AD是△ABC的BC边上的中线，E为AD的中点，连接BE并延长交AC于点F．求EF：BF．
分析 作EH∥AC交BC于H，根据三角形的中位线定理得到DH=HC，即BH=3HC，根据平行线分线段成比例定理证明结论．
解答 证明：作EH∥AC交BC于H，
∵E为AD的中点，
∴DH=HC，
∵AD是△ABC的中线，
∴BD=DC，又DH=HC，
∴BH=3HC，
∵EH∥AC，
∴$\frac{EF}{BF}$=$\frac{CH}{BC}$=$\frac{1}{4}$．
点评 本题考查的是三角形中位线定理和平行线分线段成比例定理，掌握三角形的中位线平行于第三边且等于第三边的一半、正确作出辅助线是解题的关键．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
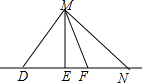在一个无风的日子，一辆汽车在直线形的公路上由A向B行驶，如图，M是学校的位置，当汽车行驶到下列哪一位置时，小学受汽车的影响最大（ ）
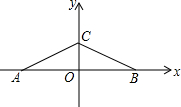如图，在直角坐标系中，有点A（-2，0）、B（2，0）、C（0，1），另有一点D与点A、B、C构成平行四边形的顶点，则点D的坐标是（4，1），（-4，1），（0，-1）．