题目内容
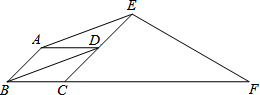 如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°,AB=2.求CF的长.
如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°,AB=2.求CF的长.考点:平行四边形的判定与性质
专题:
分析:首先证明四边形ABDE是平行四边形,可得AB=DE=CD,即D为CE中点,然后再得CE=4,再利用三角函数可求出HF和CH的长即可.
解答: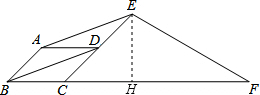 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∵AE∥DB,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,即D为CE中点,
∵AB=2,
∴CE=4,
∵AB∥CD,
∴∠ECF=∠ABC=45°,
过E作EH⊥BF于点H,
∵CE=4,∠ECF=45°,
∴EH=CH=2
,
∵∠EFC=30°,
∴FH=2
,
∴CF=2
+2
.
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴AB∥CD,AB=DC,
∵AE∥DB,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,即D为CE中点,
∵AB=2,
∴CE=4,
∵AB∥CD,
∴∠ECF=∠ABC=45°,
过E作EH⊥BF于点H,
∵CE=4,∠ECF=45°,
∴EH=CH=2
| 2 |
∵∠EFC=30°,
∴FH=2
| 6 |
∴CF=2
| 2 |
| 6 |
点评:此题主要考查了平行四边形的判定与性质,以及三角函数的应用,关键是掌握平行四边形对边相等.

练习册系列答案
相关题目
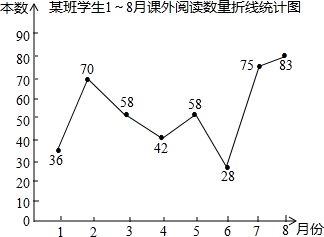 九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,与上月比较阅读数量变化率最大的月份是( )
九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,与上月比较阅读数量变化率最大的月份是( )
 如图,某登山队在山脚A处测得山顶B处的仰角为45°,沿坡角30°的斜坡AD前进1000m后到达D处,又测得山顶B处的仰角为60°.求山的高度BC.
如图,某登山队在山脚A处测得山顶B处的仰角为45°,沿坡角30°的斜坡AD前进1000m后到达D处,又测得山顶B处的仰角为60°.求山的高度BC.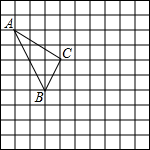 在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).
在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).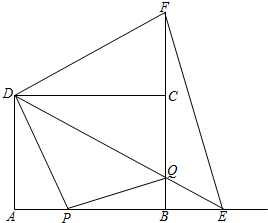 如图,矩形ABCD中,AB=8,AD=6.动点P从点A出发,沿线段AB(不包括端点A,B)以每秒2个单位长度的速度,匀速向点B运动;动点Q从点B出发,沿线段BC(不包括端点B,C)以每秒1个单位长度的速度,匀速向点C运动.连接DQ并延长交AB的延长线于点E,把DE沿DC翻折交BC延长线于点F,连接EF.点P,Q同时出发,同时停止,设运动时间为t秒.
如图,矩形ABCD中,AB=8,AD=6.动点P从点A出发,沿线段AB(不包括端点A,B)以每秒2个单位长度的速度,匀速向点B运动;动点Q从点B出发,沿线段BC(不包括端点B,C)以每秒1个单位长度的速度,匀速向点C运动.连接DQ并延长交AB的延长线于点E,把DE沿DC翻折交BC延长线于点F,连接EF.点P,Q同时出发,同时停止,设运动时间为t秒.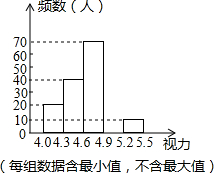 某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题: 如图,已知⊙0是△ABC的外接圆,半径长为5,点D、E分别是边AB和边AC是中点,AB=AC,BC=6.求∠OED的正切值.
如图,已知⊙0是△ABC的外接圆,半径长为5,点D、E分别是边AB和边AC是中点,AB=AC,BC=6.求∠OED的正切值.