题目内容
 如图,是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,第三行有4个点,第四行有8个点,….那么这个三角点阵中前n行的点数之和可能是( )
如图,是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,第三行有4个点,第四行有8个点,….那么这个三角点阵中前n行的点数之和可能是( )| A、510 | B、511 |
| C、512 | D、513 |
考点:规律型:图形的变化类
专题:
分析:首先由题意可知这个三角点阵中的数,从第2行起,每一行与它的前一行的数之比等于2,即点阵中的数成等比数列,第n行有2n-1个点.根据等比数列的求和公式得出这个三角点阵中前n行的点数之和为2n-1,又29=512,由此得出答案.
解答:解:∵一个三角点阵,从上向下数有无数多行,
其中第一行有1个点,1=20;
第二行有2个点,2=21;
第三行有4个点,4=22;
第四行有8个点,8=23;
…
∴第n行有2n-1个点,
∴这个三角点阵中前n行的点数之和为:
=2n-1,
又∵29=512,
∴29-1=511.
故选B.
其中第一行有1个点,1=20;
第二行有2个点,2=21;
第三行有4个点,4=22;
第四行有8个点,8=23;
…
∴第n行有2n-1个点,
∴这个三角点阵中前n行的点数之和为:
| 1(1-2n) |
| 1-2 |
又∵29=512,
∴29-1=511.
故选B.
点评:本题考查了规律型:图形的变化类,根据前面四行的点数特点,得出这个点阵中的数成等比数列,从而根据等比数列的求和公式得出这个三角点阵中前n行的点数之和为2n-1,是解题的关键.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,∠A=135°,E,F分别是边AB和BC的中点,EP⊥CD于点P,若AB=8,AD=3
如图,在平行四边形ABCD中,∠A=135°,E,F分别是边AB和BC的中点,EP⊥CD于点P,若AB=8,AD=3| 2 |
| A、4 | ||||
B、
| ||||
C、
| ||||
D、
|
计算2sin30°-cos245°的值是( )
| A、1 | B、-1 | C、0.5 | D、0 |
两圆的半径分别为3和7,圆心距为6,则两圆的交点个数为( )
| A、1个 | B、2个 |
| C、0个 | D、以上都不对 |
如果a、b是方程x2-3x+1=0的两根,那么代数式a2+2b2-3b的值为( )
| A、6 | B、-6 | C、7 | D、-7 |
一个圆锥的侧面展开图是一个圆心角为216°,面积为60π的扇形,则这个圆锥的高是( )
| A、8 | B、10 | C、12 | D、14 |
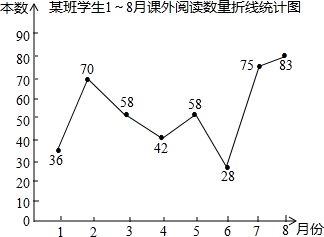 九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,与上月比较阅读数量变化率最大的月份是( )
九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,与上月比较阅读数量变化率最大的月份是( )