题目内容
6.在小学认识三角形的基础上我们来继续学习三角形.三角形可用符号“△”表示.例如图1中的三角形可记作“△ABC”;在一个三角形中,如果有两个角相等,我们新定义这个三角形为等角三角形.(1)如图1,∠ABC的角平分线交AC于D,DE∥BC交AB于E,
①请在图1中依题意补全图形;
②判断△EBD是不是等角三角形;
(2)如图2,AF是∠GAC的角平分线,AF∥BC.判断△ABC是不是等角三角形.
(3)如图3,BM,CM 分别是∠ABC 和∠ACB的角平分线,请过图中某一点,作一条图中已有线段的平行线,使图中出现一个或两个等角三角形,标出字母,并就出现的一个三角形是等角三角形说明理由.

分析 (1)①根据题意画出图形即可;
②根据角平分线定义可得∠ABD=∠DBC,根据平行线的性质可得∠EDB=∠DBC,进而可得∠EBD=∠EDB,从而可得△EBD是等角三角形;
(2)根据平行线的性质可得∠1=∠B,∠2=∠C,再根据角平分线的性质可得∠1=∠2,进而可得结论;
(3)过点M作GH∥BC,交AB于点G,交AC于点H,利用平行线的性质和角平分线定义进行证明即可.
解答 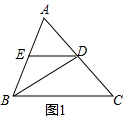 解:(1)①如图1.
解:(1)①如图1.
②△EBD是等角三角形.
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴△EBD是等角三角形;
(2)△ABC是等角三角形.
理由如下:如图2,∵AF∥BC,
∴∠1=∠B,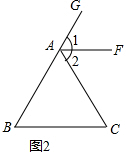 ∠2=∠C,
∠2=∠C,
∵AF是∠GAC的角平分线,
∴∠1=∠2,
∴∠B=∠C,
∴△ABC是等角三角形.
(3)过点M作GH∥BC,交AB于点G,交AC于点H.
出现两个等角三角形分别是:△GBM和△HMC.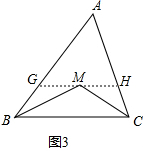
证明:如图3,∵GH∥BC,
∴∠1=∠3,
∵BM是∠ABC角平分线,
∴∠GBM=∠3,
∴∠1=∠GBM,
所以△GBM是等角三角形.
点评 此题主要考查了平行线的性质,以及角平分线的定义,关键是掌握两直线平行,内错角、同位角相等.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
14. 如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=100°,则∠EBC度数为( )
如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=100°,则∠EBC度数为( )
 如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=100°,则∠EBC度数为( )
如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于$\frac{1}{2}$GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=100°,则∠EBC度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 80° |
15.解方程组$\left\{\begin{array}{l}{17x-2y=8①}\\{13x-4y=-10②}\end{array}\right.$时,消去未知数y最简单的方法是( )
| A. | ①×4-②×2 | B. | ①×2-② | ||
| C. | 由①得y=$\frac{17x-8}{2}$,再代入② | D. | 由②得$\frac{13x+10}{4}$,再代入① |
16.某公司经过市场调研,决定从明年起对甲、乙两种产品实行“限产压库”,要求这两种产品全年共新增产量20件,这20件的总产值p(万元)满足:1100<p<1200,已知有关数据如图所示,设生产甲种产品x件,解答下列问题:
(1)求P与x的函数关系式?
(2)该公司明年应该怎样安排甲、乙两种产品的生产量?
(3)如果甲种产品每件的成本为10万元,乙种产品每件的成本为15万元生产这两种产品的总成本为y万元,请写出y与x的函数关系式,并说明x取何值时能使总成本最低?
| 产品 | 每件产品的产值 |
| 甲 | 45万元 |
| 乙 | 75万元 |
(2)该公司明年应该怎样安排甲、乙两种产品的生产量?
(3)如果甲种产品每件的成本为10万元,乙种产品每件的成本为15万元生产这两种产品的总成本为y万元,请写出y与x的函数关系式,并说明x取何值时能使总成本最低?
 如图,△ABC中,∠A=90°,O为其内心(角平分线交点),射线BO、CO交AC、AB于点D、E,连接DE,点F为DE的中点,连接OF,求证:OF⊥BC.
如图,△ABC中,∠A=90°,O为其内心(角平分线交点),射线BO、CO交AC、AB于点D、E,连接DE,点F为DE的中点,连接OF,求证:OF⊥BC.
 在如图所示的平面直角坐标系中,四边形OABC各顶点的坐标分别是
在如图所示的平面直角坐标系中,四边形OABC各顶点的坐标分别是