题目内容
11.化简:$\sqrt{48}$=4$\sqrt{3}$;$\sqrt{27{x}^{3}b}$=3x$\sqrt{3xb}$;$\sqrt{4\frac{21}{25}}$=$\frac{11}{5}$;$\sqrt{(-2)×(-8)}$=4;$\sqrt{{x}^{3}+6{x}^{2}y+9x{y}^{2}}$=|x+3y|$\sqrt{x}$.分析 根据化简二次根式的步骤:①把被开方数分解因式;②利用积的算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2进行计算.
解答 解:$\sqrt{48}$=$\sqrt{3×16}$=4$\sqrt{3}$;
$\sqrt{27{x}^{3}b}$=3x$\sqrt{3xb}$;
$\sqrt{4\frac{21}{25}}$=$\sqrt{\frac{121}{25}}$=$\frac{11}{5}$;
$\sqrt{(-2)×(-8)}$=$\sqrt{16}$=4;
$\sqrt{{x}^{3}+6{x}^{2}y+9x{y}^{2}}$=$\sqrt{x(x+3y)^{2}}$=|x+3y|$\sqrt{x}$,
故答案为:4$\sqrt{3}$;3x$\sqrt{3xb}$;$\frac{11}{5}$;4;|x+3y|$\sqrt{x}$.
点评 此题主要考查了二次根式的性质与化简,关键是掌握化简二次根式的步骤.

练习册系列答案
相关题目
1.点P(6-2a,a-1)关于y轴的对称点在第一象限,则a的取值范围是( )
| A. | a<3 | B. | 1<a<3 | C. | a>1 | D. | a>3 |
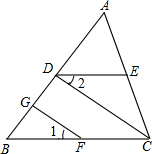 如图所示,CD⊥AB于D,DE∥BC,∠1=∠2,则FG与AB有什么位置关系?试说明理由.
如图所示,CD⊥AB于D,DE∥BC,∠1=∠2,则FG与AB有什么位置关系?试说明理由. 如图:线段NB上有一点C.
如图:线段NB上有一点C.