题目内容
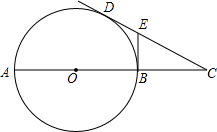 如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )
如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:切线的性质
专题:
分析:连接OD,根据切线长定理可得DE=BE,然后证明△BCE∽△DCO,则
=
=
,从而求解.
| DE |
| EC |
| BE |
| EC |
| OD |
| OC |
解答: 解:连接OD.
解:连接OD.
设DE=x,
∵CD切⊙O于点D,BE切⊙O于点B,
∴BE=DE=x,
∵∠ODC=∠EBC,∠C=∠C,
∴△BCE∽△DCO,
∴
=
=
=
,
∴
=
.
故选C.
 解:连接OD.
解:连接OD.设DE=x,
∵CD切⊙O于点D,BE切⊙O于点B,
∴BE=DE=x,
∵∠ODC=∠EBC,∠C=∠C,
∴△BCE∽△DCO,
∴
| BE |
| EC |
| OD |
| OC |
| a |
| a+na |
| 1 |
| n+1 |
∴
| DE |
| EC |
| 1 |
| n+1 |
故选C.
点评:本题考查了相似三角形的判定与性质以及切线长定理,正确作出辅助线,证明△BCE∽△DCO是关键.

练习册系列答案
相关题目
 如图,在△ABC中,AC=6cm,BC=4cm,DE垂直平分AB,则△BCD的周长为( )
如图,在△ABC中,AC=6cm,BC=4cm,DE垂直平分AB,则△BCD的周长为( )| A、8cm | B、9cm |
| C、10cm | D、11cm |
 如图,为了测量一栋楼的高度,王青同学在她脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到大楼顶部.这时∠LMK等于∠SMT吗?如果王青身高1.55m,她估计自己眼睛离地面1.50m,同时量得LM=0.30m,MS=25m,这栋大楼有多高?
如图,为了测量一栋楼的高度,王青同学在她脚下放了一面镜子,然后向后退,直到她刚好在镜子中看到大楼顶部.这时∠LMK等于∠SMT吗?如果王青身高1.55m,她估计自己眼睛离地面1.50m,同时量得LM=0.30m,MS=25m,这栋大楼有多高?