题目内容
2+
是方程x2-5xcosθ+1的两个根中的一根,θ为锐角,试求tanθ.(参考公式:sin2θ+cos2θ=1,tanθ=
)
| 3 |
| sinθ |
| cosθ |
考点:一元二次方程的解,同角三角函数的关系
专题:
分析:把x=2+
代入已知方程求得cosθ的值,然后根据参考公式得到sinθ的值,则易求tanθ.
| 3 |
解答:解:把x=2+
代入x2-5xcosθ+1=0,得
(2+
)2-5(2+
)cosθ+1=0,
解得 cosθ=
.
∵θ为锐角,
∴0<sinθ<1.
又sin2θ+cos2θ=1,
∴sin2θ+
=1,
∴sinθ=
,
∴tanθ=
=
=
.
| 3 |
(2+
| 3 |
| 3 |
解得 cosθ=
| 4 |
| 5 |
∵θ为锐角,
∴0<sinθ<1.
又sin2θ+cos2θ=1,
∴sin2θ+
| 16 |
| 25 |
∴sinθ=
| 3 |
| 5 |
∴tanθ=
| sinθ |
| cosθ |
| ||
|
| 3 |
| 4 |
点评:本题考查了一元二次方程的解的定义和同角三角函数的关系.注意:sinθ的取值范围.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
下列函数中,y随x的增大而减少的是( )
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=
|
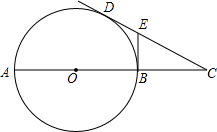 如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )
如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知线段点A、B、C在一条直线上,AB=5,BC=3,则AC的长为( )
| A、8 | B、2 | C、8或2 | D、无法确定 |




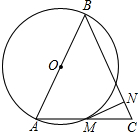 如图所示,在锐角△ABC中,AB=BC,点O是边AB的中点,以点O为圆心,OA为半径的圆交于点M,过点M作⊙O的切线MN交BC于点N.求证:CM2=CN•CB.
如图所示,在锐角△ABC中,AB=BC,点O是边AB的中点,以点O为圆心,OA为半径的圆交于点M,过点M作⊙O的切线MN交BC于点N.求证:CM2=CN•CB.


