题目内容
已知α+β=2,则α2-β2+4β= .
考点:完全平方公式
专题:
分析:先根据平方差公式分解,代入后合并同类项,最后再代入求出即可.
解答:解:∵α+β=2,
∴α2-β2+4β
=(α+β)(α-β)+4β
=2(α-β)+4β
=2α+2β
=2(α+β)
=2×2
=4,
故答案为:4.
∴α2-β2+4β
=(α+β)(α-β)+4β
=2(α-β)+4β
=2α+2β
=2(α+β)
=2×2
=4,
故答案为:4.
点评:本题考查了平方差公式的应用,主要考查学生运用公式进行计算的能力,用了整体代入思想.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
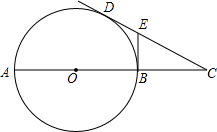 如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )
如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,sin A=
如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,sin A=| 3 |
| 5 |
| A、3,15 | B、4,20 |
| C、5,25 | D、4,15 |
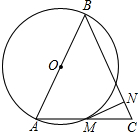 如图所示,在锐角△ABC中,AB=BC,点O是边AB的中点,以点O为圆心,OA为半径的圆交于点M,过点M作⊙O的切线MN交BC于点N.求证:CM2=CN•CB.
如图所示,在锐角△ABC中,AB=BC,点O是边AB的中点,以点O为圆心,OA为半径的圆交于点M,过点M作⊙O的切线MN交BC于点N.求证:CM2=CN•CB. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF. 将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为多少?
将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为多少?


