题目内容
一个直角三角形的周长是24cm,面积是24cm2,则斜边的长为 .
考点:勾股定理
专题:
分析:首先利用直角三角形的性质设两直角边长分别为a,b,得出斜边长为:24-a-b,其面积为:
ab=24,再利用勾股定理得出a+b的值,进而得出答案.
| 1 |
| 2 |
解答:解:设两直角边长分别为a,b,则斜边长为:24-a-b,
其面积为:
ab=24,
故ab=48,
∵a2+b2=(24-a-b)2,
整理得:a2+b2=576+(a+b)2-48(a+b)
0=576+2ab-48(a+b)
故0=576+96-48(a+b)
解得:a+b=14,
∴斜边的长为:24-14=10.
故答案为:10.
其面积为:
| 1 |
| 2 |
故ab=48,
∵a2+b2=(24-a-b)2,
整理得:a2+b2=576+(a+b)2-48(a+b)
0=576+2ab-48(a+b)
故0=576+96-48(a+b)
解得:a+b=14,
∴斜边的长为:24-14=10.
故答案为:10.
点评:此题主要考查了勾股定理以及完全平方公式的应用,熟练应用完全平方公式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
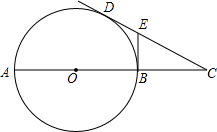 如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )
如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知线段点A、B、C在一条直线上,AB=5,BC=3,则AC的长为( )
| A、8 | B、2 | C、8或2 | D、无法确定 |
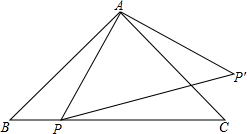 如图,△ABC是等腰三角形,点P是斜边AB上一点,将△CAP绕点C逆时针旋转90°至△CBP′的位置,若AC=2
如图,△ABC是等腰三角形,点P是斜边AB上一点,将△CAP绕点C逆时针旋转90°至△CBP′的位置,若AC=2 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=8,ON,CD分别为两圆的半径,求阴影部分的面积.
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=8,ON,CD分别为两圆的半径,求阴影部分的面积. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.