题目内容
 如图,在笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=(
如图,在笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=(| 3 |
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离.(友情提示:结果都保留根号)
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)过点P作PD⊥AB于点D,设PD=xkm,先解Rt△PBD,用含x的代数式表示BD,再解Rt△PAD,用含x的代数式表示AD,然后根据BD+AD=AB,列出关于x的方程,解方程即可;
(2)过点B作BF⊥AC于点F,先解Rt△ABF,得出BF=
AB=1km,再解Rt△BCF,得出BC=
BF.
(2)过点B作BF⊥AC于点F,先解Rt△ABF,得出BF=
| 1 |
| 2 |
| 2 |
解答: 解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,
∴BD=PD=xkm.
在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,
∴AD=
PD=
xkm.
∵BD+AD=AB,
∴x+
x=
+1,
x=1,
∴点P到海岸线l的距离为1km;
(2)如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=
AB=
km.
在△ABC中,∠C=180°-∠BAC-∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=
BF=
km,
∴点C与点B之间的距离为
km.
 解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,
∴BD=PD=xkm.
在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,
∴AD=
| 3 |
| 3 |
∵BD+AD=AB,
∴x+
| 3 |
| 3 |
x=1,
∴点P到海岸线l的距离为1km;
(2)如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=
| 1 |
| 2 |
| ||
| 2 |
在△ABC中,∠C=180°-∠BAC-∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=
| 2 |
| ||||
| 2 |
∴点C与点B之间的距离为
| ||||
| 2 |
点评:本题考查了解直角三角形的应用-方向角问题,难度适中.通过作辅助线,构造直角三角形是解题的关键.

练习册系列答案
相关题目
 如图,C为线段AB的中点,点D分线段AB的长度为2:3,已知CD=1cm,求AB的长.
如图,C为线段AB的中点,点D分线段AB的长度为2:3,已知CD=1cm,求AB的长.
 如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H.
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.点P从C点出发,沿线段CO以5个单位/秒的速度向终点O匀速运动,过点P作PH⊥OB,垂足为H.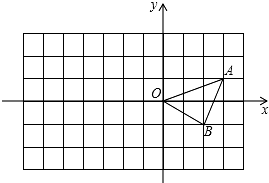 如图,已知O是坐标原点,A、B的坐标分别为(3,1),(2,-1).
如图,已知O是坐标原点,A、B的坐标分别为(3,1),(2,-1).