题目内容
1．
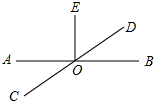如图AB、CD交于点O，OE⊥AB于O，则下列不正确的是（ ）| A． | ∠AOC与∠BOD是对顶角 | B． | ∠BOD和∠DOE互为余角 | ||
| C． | ∠AOC和∠DOE互为余角 | D． | ∠AOE和∠BOC是对顶角 |
分析 根据垂直的定义以及对顶角相等和互为余角的定义对各选项分析判断即可得解．
解答 解：A、∠AOC与∠BOD是对顶角正确，故本选项错误；
B、∵OE⊥AB，
∴∠BOE=90°，
∴∠BOD和∠DOE互为余角正确，故本选项错误；
C、∵∠AOC=∠BOD（对顶角相等），∠BOD和∠DOE互为余角，
∴∠AOC和∠DOE互为余角正确，故本选项错误；
D、应为∠AOD和∠BOC是对顶角，故本选项正确．
故选D．
点评 本题考查了对顶角相等的性质，互为余角的定义，熟记性质与概念并准确识图，理清图中各角度之间的关系是解题的关键．
练习册系列答案
相关题目
12．在Rt△ABC中，∠C=90°，a=5，c=13，则b的长为（ ）
| A． | 10 | B． | 11 | C． | 12 | D． | 13 |
16．下列计算：（1）34÷35=$\frac{1}{3}$；（2）（$\frac{1}{2012}$）0=（-2012）0；（3）（a-2）5÷（a-5）2=1；（4）x4÷x9=x-5，其中正确的有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
13．下列实数中，属于无理数的是（ ）
| A． | -$\frac{1}{3}$ | B． | 0.1 | C． | $\sqrt{4}$ | D． | $\root{3}{9}$ |
11．
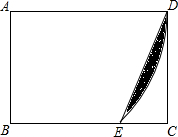在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（ ）
在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（ ）| A． | $\frac{π}{2}$-$\sqrt{2}$ | B． | $\frac{π}{2}$-$\frac{\sqrt{2}}{2}$ | C． | π-$\sqrt{2}$ | D． | π-$\frac{\sqrt{2}}{2}$ |