题目内容
20.若直线y=ax+b的图象与直线y=2x+1垂直,且经过y=4-3x和y=2x-1的交点,则b的值是$\frac{3}{2}$.分析 根据两直线垂直可知a=-$\frac{1}{2}$,然后再求得y=4-3x和y=2x-1的交点坐标,将该点坐标代入y=-$\frac{1}{2}x$+b可求得b的值.
解答 解:∵直线y=ax+b的图象与直线y=2x+1垂直,
∴a=-$\frac{1}{2}$.
将y=4-3x和y=2x-1联立得:$\left\{\begin{array}{l}{y=4-3x}\\{y=2x-1}\end{array}\right.$.
解得:$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
将x=1,y=1代入y=-$\frac{1}{2}x$+b得:$-\frac{1}{2}$+b=1.
解得:b=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题主要考查的是两直线相交或平行问题,明确相互垂直的两条直线的一次项系数为之积为-1是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在△ABC中,AB=AC,在BC上取点D,使∠BAD=50°,在AC上取AE=AD,连接DE,求∠CDE的度数.
在△ABC中,AB=AC,在BC上取点D,使∠BAD=50°,在AC上取AE=AD,连接DE,求∠CDE的度数.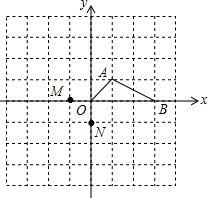 如图,在平面直角坐标系中有A(1,1)、B(3,0)两点.
如图,在平面直角坐标系中有A(1,1)、B(3,0)两点.