题目内容
11.先化简,再求值:($\frac{2x{y}^{2}}{x+y}$)3÷($\frac{x{y}^{3}}{{x}^{2}-{y}^{2}}$)2÷[$\frac{1}{2(x-y)}$]2,其中x=-$\frac{1}{2}$,y=$\frac{3}{2}$.分析 先进行乘方运算,再把除法运算转化为乘法运算,然后约分得到原式=$\frac{32(x-y)^{4}}{x+y}$,然后把x和y的值代入计算即可.
解答 解:原式=$\frac{8{x}^{3}{y}^{6}}{(x+y)^{3}}$•$\frac{(x-y)^{2}•(x+y)^{2}}{{x}^{2}{y}^{6}}$•4(x-y)2
=$\frac{32(x-y)^{4}}{x+y}$,
当x=-$\frac{1}{2}$,y=$\frac{3}{2}$,原式=$\frac{32×(-\frac{1}{2}-\frac{3}{2})^{4}}{-\frac{1}{2}+\frac{3}{2}}$=512.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式

练习册系列答案
相关题目
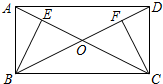 已知:如图,平行四边形ABCD的两条对角线相交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.且BE=CF.求证:平行四边形ABCD是矩形.
已知:如图,平行四边形ABCD的两条对角线相交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.且BE=CF.求证:平行四边形ABCD是矩形. 已知,如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CG=EG,求证:CD=AE.
已知,如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CG=EG,求证:CD=AE.