Question

15．在平面直角坐标系中，已知A（-1，-1）、B（2，3），若要在x轴上找一点P，使|AP-BP|最长，则点P的坐标为（-2.5，0）．

Answer 1

分析 根据题意画出坐标系，在坐标系内找出A、B两点，作点A关于x轴的对称点A′，作射线BA′交x轴于点P，求出P点坐标即可．

解答 解：如图所示：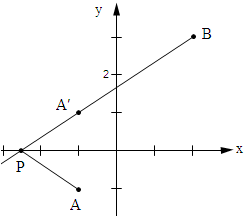

∵点A与点A′关于x轴对称，A（-1，-1），
∴A′（-1，1）．
设直线A′B的解析式为y=kx+b（k≠0），
将点B与点A′的坐标代入得：$\left\{\begin{array}{l}{2k+b=3}\\{-k+b=1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=\frac{5}{3}}\end{array}\right.$
∴直线BA′的解析式为y=$\frac{2}{3}x+\frac{5}{3}$．
将y=0代入得：$\frac{2}{3}x+\frac{5}{3}$=0．
解得：x=-2.5．
∴点P的坐标为（-2.5，0）．
故答案为：（-2.5，0）．

点评 本题考查的是轴对称的性质，根据轴对称的性质确定出点P的位置是解答此题的关键．