题目内容
11.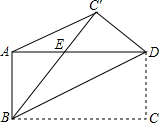 如图,将矩形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,连接AC′
如图,将矩形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,连接AC′(1)判断AC′与BD的位置关系并证明你的结论.
(2)求三角形BDE的面积.
分析 (1)由矩形的性质和折叠的性质得出∠C′BD=∠DBC=∠BDA,可得DE=BE,证出AE=C′E,得出AE:DE=C′E:BE,即可得出结论;
(2)设DE=x,则AE=8-x.根据勾股定理求BE及DE的长,即可求出△BDE的面积.
解答 解:(1)AC′∥BD;理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠DBC=∠BDA,
由折叠的性质得:∠C′BD=∠DBC,BC′=BC,
∴∠C′BD=∠BDA,BC′=AD,
∴DE=BE,
∴AE=C′E,
∴AE:DE=C′E:BE,
∴AC′∥BD;
(2)设DE=BE=x,则AE=8-x.
在△ABE中,x2=42+(8-x)2.
解得:x=5.
∴DE=5,
∴S△BDE=$\frac{1}{2}$×5×4=10.
点评 此题考查了折叠变换的性质、矩形的性质、勾股定理、平行线的判定、等腰三角形的判定;熟练掌握矩形和翻折变换的性质,证明DE=BE是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19. 如图,直线AB∥CD,AD平分∠BAC,若∠ADC=30°,则∠DCE的度数为( )
如图,直线AB∥CD,AD平分∠BAC,若∠ADC=30°,则∠DCE的度数为( )
 如图,直线AB∥CD,AD平分∠BAC,若∠ADC=30°,则∠DCE的度数为( )
如图,直线AB∥CD,AD平分∠BAC,若∠ADC=30°,则∠DCE的度数为( )| A. | 30° | B. | 50° | C. | 60° | D. | 70° |
 如图,已知ED∥AC,∠EDF=∠A,∠FDC=30°.求∠B的度数.
如图,已知ED∥AC,∠EDF=∠A,∠FDC=30°.求∠B的度数. 解不等式,并把解集表示在数轴上.
解不等式,并把解集表示在数轴上.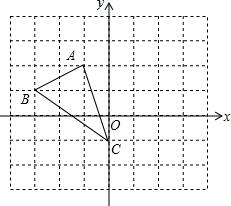 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1).