题目内容
5.若整数a能被整数b整除,则一定存在整数n,使得$\frac{a}{b}=n$,即a=bn.例如若整数a能被整数3整除,则一定存在整数n,使得$\frac{a}{3}=n$,即a=3n.(1)若一个多位自然数的末三位数字所表示的数与末三位数以前的数字所表示的数之差(大数减小数)能被13整除,那么原多位自然数一定能被13整除.例如:将数字306371分解为306和371,因为371-306=65,65是13的倍数,所以306371能被13整除.请你证明任意一个四位数都满足上述规律.
(2)如果一个自然数各数位上的数字从最高位到个位仅有两个数交替排列组成,那么我们把这样的自然数叫做“摆动数”,例如:自然数12121212从最高位到个位是由1和2交替出现组成,所以12121212是“摆动数”,再如:656,9898,37373,171717,…,都是“摆动数”,请你证明任意一个6位摆动数都能被13整除.
分析 (1)设一个四位数的末三位数为B,末三位数以前的数为A,根据题意可得A=13n+B,即这个四位数是1000(13n+B)+B=13(1000n+77B),可得;
(2)设任意一个6位摆动数的十位数字为a、个位数字为b,表示出末三位数为100b+10a+b,末三位数以前的数为100a+10b+a,将二者相减分解出因数13可得.
解答 解:(1)设一个四位数的末三位数为B,末三位数以前的数为A,
则这个四位数为:1000A+B,
由题意:A-B=13n(n为整数),
∴A=13n+B,
从而1000A+B=1000(13n+B)+B
=13000n+1001B
=13(1000n+77B),
∴这个四位数能被13整除
∴任意一个四位数都满足上述规律;
(2)设任意一个6位摆动数的十位数字为a,个位数字为b,
所以这个6位摆动数的末三位数为:100b+10a+b,
末三位数以前的数为:100a+10b+a,
∵100a+10b+a-(100b+10a+b)=91a-91b=13(7a-7b)
∴这个6位摆动数的末三位数以前的数与末三位数之差能被13整除,
∴任意一个6位摆动数能被13整除.
点评 此题主要考查了数的整除性,根据题意用未知数表示出各数是解题关键.

练习册系列答案
相关题目
20.为了解某市七年级15000名学生的体重情况,从中抽查了500名学生的体重,就这个问题来说,下列说法正确的是( )
| A. | 15000名学生的总体 | B. | 每个学生是个体 | ||
| C. | 500名学生是所抽取的一个样本 | D. | 样本容量是500 |
17.分式$-\frac{1}{{6{x^2}y}}$和$\frac{1}{2xyz}$最简公分母是( )
| A. | -6xyz | B. | 6x2yz | C. | 12xyz | D. | 12x2yz |
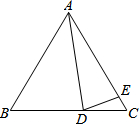 在△ABC中,AB=AC,∠BAD=40°,AE=AD,求∠EDC的度数.
在△ABC中,AB=AC,∠BAD=40°,AE=AD,求∠EDC的度数.