题目内容
若关于x的方程x4-16x3+(81-2a)x2+(16a-142)x+a2-21a+68=0的各根为整数,求a的值,并解此方程.
考点:一元二次方程的整数根与有理根
专题:
分析:首先将原式分解因式,进而得出
,进而求出a的值,即可得出方程的根.
|
解答:解:∵x4-16x3+(81-2a)x2+(16a-142)x+a2-21a+68
=(x4-16x3+60x2)+(21-2a)x2+(16a-142)x+(a2-21a+68)
=(x2-6x)(x2-10x)+[(4-a)+(17-a)]x2-[10(4-a)+6(17-a)]x+(4-a)(17-a)
=(x2-6x)(x2-10x)+[(4-a)x2-10(4-a)x]+[(17-a)x2-6(17-a)x]+(4-a)(17-a)
=(x2-6x)(x2-10x)+(4-a)(x2-10x)+(17-a)(x2-6x)+(4-a)(17-a)
=[(x2-6x)(x2-10x)+(4-a)(x2-10x)]+[(17-a)(x2-6x)+(4-a)(17-a)]
=(x2-6x+4-a)(x2-10x)+(17-a)(x2-6x+4-a)
=(x2-6x+4-a)(x2-10x+17-a)
∴
,
∴①式判别式△1=(-6)2-4(4-a)=4(a+5)
②式判别式△2=(-10)2-4(17-a)=4(a+8)
∵方程的各根为整数
∴a+5和a+8应该是整数的平方
∴设n、m∈Z且n>m≥0,且有:
,
两式相减得:3=1×3=n2-m2=(n-m)(n+m)
∴
,
解得:
,
故解得:a=-4
将a=-4代入方程①②得:
,
解③④得:x1=2,x2=4,x3=3,x4=7.
=(x4-16x3+60x2)+(21-2a)x2+(16a-142)x+(a2-21a+68)
=(x2-6x)(x2-10x)+[(4-a)+(17-a)]x2-[10(4-a)+6(17-a)]x+(4-a)(17-a)
=(x2-6x)(x2-10x)+[(4-a)x2-10(4-a)x]+[(17-a)x2-6(17-a)x]+(4-a)(17-a)
=(x2-6x)(x2-10x)+(4-a)(x2-10x)+(17-a)(x2-6x)+(4-a)(17-a)
=[(x2-6x)(x2-10x)+(4-a)(x2-10x)]+[(17-a)(x2-6x)+(4-a)(17-a)]
=(x2-6x+4-a)(x2-10x)+(17-a)(x2-6x+4-a)
=(x2-6x+4-a)(x2-10x+17-a)
∴
|
∴①式判别式△1=(-6)2-4(4-a)=4(a+5)
②式判别式△2=(-10)2-4(17-a)=4(a+8)
∵方程的各根为整数
∴a+5和a+8应该是整数的平方
∴设n、m∈Z且n>m≥0,且有:
|
两式相减得:3=1×3=n2-m2=(n-m)(n+m)
∴
|
解得:
|
故解得:a=-4
将a=-4代入方程①②得:
|
解③④得:x1=2,x2=4,x3=3,x4=7.
点评:此题主要考查了一元二次方程的整数根与有理根,正确将原方程分解因式是解题关键.

练习册系列答案
相关题目
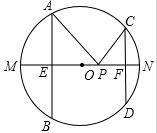 如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值.
如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值. 如图,△ODC中,∠D=90°,EC是∠DCO的平分线,OE⊥CE,点E作EF⊥OC于点F,判断EF与OD之间的数量关系,并加以证明.
如图,△ODC中,∠D=90°,EC是∠DCO的平分线,OE⊥CE,点E作EF⊥OC于点F,判断EF与OD之间的数量关系,并加以证明.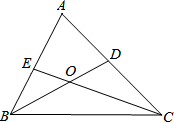 如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.
如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O. 如图,AB∥CD,AB交MN于F,FG平分∠MFB,FH平分∠AFG,CD与MN交于E,若∠BFG:∠HFM=1:3,则∠CEM的度数是
如图,AB∥CD,AB交MN于F,FG平分∠MFB,FH平分∠AFG,CD与MN交于E,若∠BFG:∠HFM=1:3,则∠CEM的度数是