题目内容
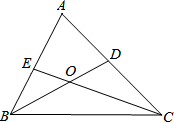 如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.
如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.(1)当∠ABC=60°,∠ACB=80°时,求∠BOC的度数.
(2)当∠A=40°时,求∠BOC的度数.
(3)当∠A=x0时,求∠BOC的度数(用含x代数式表示).
考点:三角形内角和定理
专题:
分析:(1)先根据角平分线的性质得出∠OBC与∠OCB的度数,再根据三角形内角和定理即可得出结论;
(2)先根据∠A=40°求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠OBC+∠OCB的度数,根据三角形内角和定理即可得出结论;
(3)根据∠A=x°求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠OBC+∠OCB的度数,根据三角形内角和定理即可得出结论.
(2)先根据∠A=40°求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠OBC+∠OCB的度数,根据三角形内角和定理即可得出结论;
(3)根据∠A=x°求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠OBC+∠OCB的度数,根据三角形内角和定理即可得出结论.
解答:解:(1)∵在△ABC中,∠ABC=60°,∠ACB=80°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC=
∠ABC=
×60°=30°,∠OCB=
∠ACB=
×80°=40°,
∴∠BOC=180°-∠OBC-∠OCB=180°-30°-40°=110°;
(2)∵在△ABC中,∠A=40°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°-40°)=70°,
∴∠BOC=180°-70°=110°;
(3)在△ABC中,∠A=x°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°-x°)=90°-
x°,
∴∠BOC=180°-(90°-x°)=90°+
x°.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-∠OBC-∠OCB=180°-30°-40°=110°;
(2)∵在△ABC中,∠A=40°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-70°=110°;
(3)在△ABC中,∠A=x°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(90°-x°)=90°+
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
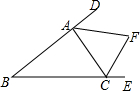 如图,已知∠CAD和∠ACE的平分线AF、CF相交于点F.求证:点F在∠DBE的角平分线上.
如图,已知∠CAD和∠ACE的平分线AF、CF相交于点F.求证:点F在∠DBE的角平分线上. 如图所示:在平面直角坐标系中,网格中每一个小正方形的边长为l个单位长度;
如图所示:在平面直角坐标系中,网格中每一个小正方形的边长为l个单位长度;