Question

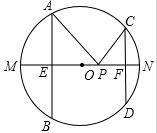如图，AB、CD是半径为10的圆O的两条弦，AB=16，CD=12，MN是直径，AB⊥MN于点E，CD⊥MN于F，P为EF上任意一点，求PA+PC的最小值．

Answer 1

考点：轴对称-最短路线问题,勾股定理,垂径定理

专题：

分析：根据轴对称确定最短路线问题，连接AD，与MN的交点即为所求的PA+PC的最小值时的点P，根据垂径定理求出AE、CF，利用勾股定理列式求出OE、OF，过点D作DH⊥AB于H，求出AH、DH，再利用勾股定理列式计算即可得解．

解答：解：∵AB⊥MN，CD⊥MN，
∴连接AD，与MN的交点即为所求的PA+PC的最小值时的点P，
由垂径定理得，AE=

1

2

AB=

1

2

×16=8，
CF=

1

2

CD=

1

2

×12=6，
∵⊙O的半径为10，
∴OE=

102-82

=6，
OF=

102-62

=8，
过点D作DH⊥AB于H，则AH=AE+EH=8+6=14，
DH=OE+OF=6+8=14，
∴AD=

142+142

=14

2

，
即PA+PC的最小值是14

2

．

点评：本题考查了轴对称确定最短路线问题，垂径定理，勾股定理，熟记各定理并确定出PA+PC最小时的点判定位置是解题的关键．