题目内容
14.阅读下列材料:∵$\sqrt{9}<\sqrt{11}<\sqrt{16}$,
∴$3<\sqrt{11}<4$,
∴$\sqrt{11}$的整数部分为3,小数部分为$(\sqrt{11}-3)$.
请你观察上述的规律后试解下面的问题:
如果9π的整数部分为a,$\root{3}{28}$的小数部分为b,求a+b的值.
分析 由9π≈28.26,可得其整数部分a=28,由27<28<64,可得$\root{3}{27}$<$\root{3}{28}$<$\root{3}{64}$,可得3$<\root{3}{28}$<4,可得$\root{3}{28}$的小数部分b=$\root{3}{28}$-3,可得a+b的值.
解答 解:∵9π≈28.26,
∴a=28,
∵27<28<64,
∴$\root{3}{27}$<$\root{3}{28}$<$\root{3}{64}$,
∴3$<\root{3}{28}$<4,
∴b=$\root{3}{28}$-3,
∴a+b=28+$\root{3}{28}$-3=25$+\root{3}{28}$,
∴a+b的值为25$+\root{3}{28}$.
点评 本题主要考查了估算无理数的大小,根据题意估算出a,b的值是解答此题的关键.

练习册系列答案
相关题目
2.下列命题中,假命题是( )
| A. | 如果两条直线都与第三条直线平行,那么这两条直线也互相平行 | |
| B. | 两条直线被第三条直线所截,同旁内角互补 | |
| C. | 两直线平行,内错角相等 | |
| D. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 |
6.某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系.
(1)试求y与x之间的函数表达式.
(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式.
(毛利润=销售总价-成本总价)
| X(元/件) | 35 | 40 | 45 | 50 | 55 |
| Y(件) | 550 | 500 | 450 | 400 | 350 |
(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式.
(毛利润=销售总价-成本总价)
 如图所示,直线l1∥l2,AB⊥D于点E,如果∠1=34°,求∠2的度数.
如图所示,直线l1∥l2,AB⊥D于点E,如果∠1=34°,求∠2的度数.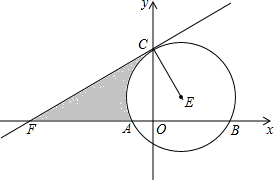 如图,半径为2的⊙E交x轴于A、B,交y轴于点C、D,直线CF交x轴负半轴于点F,连接EC.已知点E的坐标为(1,1),∠OFC=30°.
如图,半径为2的⊙E交x轴于A、B,交y轴于点C、D,直线CF交x轴负半轴于点F,连接EC.已知点E的坐标为(1,1),∠OFC=30°. 完成下面的证明.
完成下面的证明.