当m=10时.关于x的方程$\frac{2x}{x-5}$=$\frac{m}{x-5}$+3会产生增根．题目和参考答案——青夏教育精英家教网—

题目内容

3．当m=10时，关于x的方程$\frac{2x}{x-5}$=$\frac{m}{x-5}$+3会产生增根．

分析分式方程去分母转化为整式方程，由分式方程有增根，得到x-5=0，求出x的值代入整式方程即可求出m的值．

解答解：去分母得：2x=m+3x-15，
由分式方程有增根，得到x-5=0，即x=5，
把x=5代入整式方程得：10=m+15-15，
解得：m=10，
故答案为：10

点评此题考查了分式方程的增根，增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．

练习册系列答案

相关题目

13．

如图，若在象棋盘上建立直角坐标系，使“帅”位于点（-1，-2），则“兵”位于点（　　）

14．阅读下列材料：
∵$\sqrt{9}＜\sqrt{11}＜\sqrt{16}$，
∴$3＜\sqrt{11}＜4$，
∴$\sqrt{11}$的整数部分为3，小数部分为$（\sqrt{11}-3）$．
请你观察上述的规律后试解下面的问题：
如果9π的整数部分为a，$\root{3}{28}$的小数部分为b，求a+b的值．

11．化简二次根式$\sqrt{-\frac{1}{x}}$（x＜0），得（　　）

A．

$\frac{{\sqrt{x}}}{x}$

B．

$\frac{{\sqrt{-x}}}{x}$

C．

$-\frac{{\sqrt{-x}}}{x}$

D．

$-\frac{{\sqrt{x}}}{x}$

18．计算题：
（1）$\sqrt{12}+\sqrt{48}-\sqrt{75}$
（2）$\frac{{\sqrt{72}-\sqrt{16}}}{{\sqrt{8}}}-{（{\sqrt{2}-1}）^2}$
（3）$2sin30°+\sqrt{3}tan60°+2{cos^2}45°$．

8．相交两圆的圆心距是5cm，其中一圆半径是3cm，则另一圆的半径可能是（　　）

15．

如图，在4×4的正方形网格中，若将△ABC绕着点A逆时针旋转得到△AB′C′，则$\widehat{BB′}$的长为π．

12．

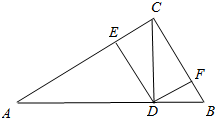如图，CD是Rt△ABC斜边AB上的高，DE⊥AC，DF⊥BC，垂足分别为E，F．已知AC=8，BC=6．
（1）求$\frac{DF}{DE}$的值；
（2）求四边形DECF的面积．

10．

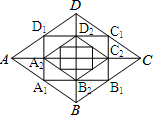如图，菱形ABCD的对角线长分别为a、b，以菱形ABCD各边的中点为顶点作矩形A₁B₁C₁D₁，然后再以矩形A₁B₁C₁D₁的中点为顶点作菱形A₂B₂C₂D₂，…，如此下去，得到四边形A₂₀₁₁B₂₀₁₁C₂₀₁₁D₂₀₁₁的面积用含a，b的代数式表示为$\frac{ab}{{2}^{2012}}$．

试题分类