题目内容
19. 完成下面的证明.
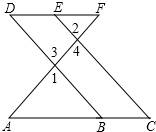
完成下面的证明.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.
证明:∵∠1=∠2(已知),∠1=∠3,∠2=∠4 (对顶角相等)
∴∠3=∠4(等量代换).
∴DB∥CE(内错角相等,两直线平行 )
∴∠C=∠ABD (两直线平行,同位角相等 )
∵∠C=∠D (已知 )
∴∠D=∠ABD (等量代换 )
∴AC∥DF (内错角相等,两直线平行 )
分析 根据对顶角相等得∠2=∠4,和已知条件∠1=∠2,利用等量代换得∠1=∠4,而∠1=∠3,所以∠3=∠4,根据平行线的判定得到BD∥CE,然后根据平行线的性质有∠C=∠ABD;由已知条件
∠C=∠D,利用等量代换得∠D=∠ABD,然后根据平行线的判定方法即可得到AC∥DF.
解答 解:∵∠1=∠2(已知),∠1=∠3,∠2=∠4 (对顶角相等)
∴∠3=∠4(等量代换).
∴DB∥CE( 内错角相等,两直线平行 )
∴∠C=∠ABD ( 两直线平行,同位角相等 )
∵∠C=∠D ( 已知 )
∴∠D=∠ABD ( 等量代换 )
∴AC∥DF ( 内错角相等,两直线平行 )
故答案是:对顶角相等;DB;CE;内错角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
点评 本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等.

练习册系列答案
相关题目
11.化简二次根式$\sqrt{-\frac{1}{x}}$(x<0),得( )
| A. | $\frac{{\sqrt{x}}}{x}$ | B. | $\frac{{\sqrt{-x}}}{x}$ | C. | $-\frac{{\sqrt{-x}}}{x}$ | D. | $-\frac{{\sqrt{x}}}{x}$ |
8.相交两圆的圆心距是5cm,其中一圆半径是3cm,则另一圆的半径可能是( )
| A. | 1cm | B. | 8cm | C. | 4cm | D. | 2cm |
9.如果一个多边形的每个内角都相等,且内角和为1260°,那么这个多边形的一个外角等于( )
| A. | 30° | B. | 36° | C. | 40° | D. | 45° |
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b和x轴上,已知点B1(1,1),B2(3,2),则B4的坐标(15,8),Bn的坐标(2n-1,2n-1).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b和x轴上,已知点B1(1,1),B2(3,2),则B4的坐标(15,8),Bn的坐标(2n-1,2n-1).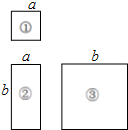 如图,有三种卡片①②③若干张,①是边长为a的小正方形,②是长为b宽为a的长方形,③是边长为b的大正方形.
如图,有三种卡片①②③若干张,①是边长为a的小正方形,②是长为b宽为a的长方形,③是边长为b的大正方形.