题目内容
6.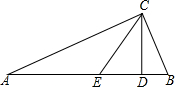 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CE是△ABC的中线,∠BCD=22.5°.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CE是△ABC的中线,∠BCD=22.5°.(1)求∠CED的度数;
(2)若CD=1,求△ABC的面积.
分析 (1)先根据CD⊥AB于点D得出∠CDB=90°,由∠BCD=22.5°即可得出∠B的度数,根据在Rt△ABC中,∠ACB=90°,CE是△ABC的中线可知CE=AE=BE,故可得出∠BCE=∠B,根据三角形内角和定理即可得出∠CED的度数;
(2)由(1)可知∠CED=45°,故可得出△CED是等腰直角三角形,根据勾股定理可得出CE的长,进而得出AB的长,根据三角形的面积公式即可得出结论.
解答 解:(1)∵CD⊥AB于点D,
∴∠CDB=90°.
∵∠BCD=22.5°,
∴∠B的度数=67.5°.
在Rt△ABC中,
∵∠ACB=90°,CE是△ABC的中线,
∴CE=AE=BE,
∴∠BCE=∠B=67.5°,
∴∠CED=180°-2×67.5°=45°;
(2)∵由(1)可知∠CED=45°,
∴△CED是等腰直角三角形,
∴DE=CD=1,
∴CE=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴AB=2CE=2$\sqrt{2}$,
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×2$\sqrt{2}$×1=$\sqrt{2}$.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
17.下列计算正确的是( )
| A. | $\sqrt{4}$$+\sqrt{(-2)^{2}}$=0 | B. | $\sqrt{\frac{3}{2}}$$-\sqrt{\frac{2}{3}}$=0 | C. | $\sqrt{6}$$÷\sqrt{3}$=2 | D. | $\sqrt{6}$×$\sqrt{\frac{3}{2}}$=3 |
14.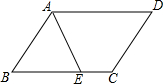 如图,在?ABCD中,AE平分∠BAD交边BC于点E,若AD=8,EC=2,则AB的长是( )
如图,在?ABCD中,AE平分∠BAD交边BC于点E,若AD=8,EC=2,则AB的长是( )
 如图,在?ABCD中,AE平分∠BAD交边BC于点E,若AD=8,EC=2,则AB的长是( )
如图,在?ABCD中,AE平分∠BAD交边BC于点E,若AD=8,EC=2,则AB的长是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
11.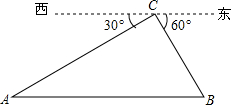 笔直的公路AB一侧有加油站C,已知从西面入口点A到C的距离为60米,西东两个入口A、B与加油站C之间的方向角如图所示,则A、B两个入口间的距离为( )
笔直的公路AB一侧有加油站C,已知从西面入口点A到C的距离为60米,西东两个入口A、B与加油站C之间的方向角如图所示,则A、B两个入口间的距离为( )
 笔直的公路AB一侧有加油站C,已知从西面入口点A到C的距离为60米,西东两个入口A、B与加油站C之间的方向角如图所示,则A、B两个入口间的距离为( )
笔直的公路AB一侧有加油站C,已知从西面入口点A到C的距离为60米,西东两个入口A、B与加油站C之间的方向角如图所示,则A、B两个入口间的距离为( )| A. | 20$\sqrt{3}$米 | B. | 30$\sqrt{3}$米 | C. | 40$\sqrt{3}$米 | D. | 60$\sqrt{3}$米 |
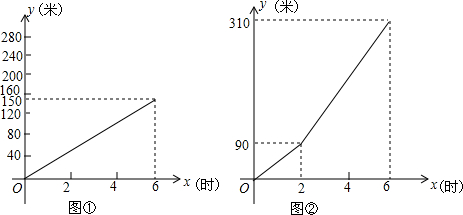
 如图,已知正方形ABCD的边长为4,点E在边AB上,且AE=1;点F为边CD上一动点,且DF=m.以A为原点,AB所在直线为x轴建立平面直角坐标系.
如图,已知正方形ABCD的边长为4,点E在边AB上,且AE=1;点F为边CD上一动点,且DF=m.以A为原点,AB所在直线为x轴建立平面直角坐标系. 自从上次赛跑乌龟大胜兔子后,乌龟便成了体育界的名人,又是广告,又是讲演,活动不断,可蚂蚁偏偏不服气,向乌龟下了挑战书,我们来看:
自从上次赛跑乌龟大胜兔子后,乌龟便成了体育界的名人,又是广告,又是讲演,活动不断,可蚂蚁偏偏不服气,向乌龟下了挑战书,我们来看: