题目内容
14．
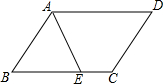如图，在?ABCD中，AE平分∠BAD交边BC于点E，若AD=8，EC=2，则AB的长是（ ）| A． | 10 | B． | 8 | C． | 6 | D． | 4 |
分析 利用平行四边形的性质以及角平分线的性质得出∠BAE=∠BEA，进而得出AB=BE，又因为BE=BC-CE=6，所以AB=6，问题得解．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC=8，
∵AE平分∠BAD交边BC于点E，
∴∠BAE=∠DAE，
∵AD∥BC，
∴∠DAE=∠BEA，
∴∠BAE=∠BEA，
∴AB=BE，
∴AB=BE=BC-CE=6，
故选：C．
点评 本题考查平行四边形的性质以及等腰三角形的判定和性质角平分线的定义，解题关键是知道平行四边形中对边平行，对边相等，从而可求出结果．
练习册系列答案
学业测评一课一测系列答案
相关题目
4．若等腰三角形的周长为20，有一边长为4，则它的腰长为（ ）
| A． | 4 | B． | 8 | C． | 10 | D． | 4或8 |
2．
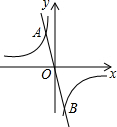如图，反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A（-2，4），B两点，若$\frac{{k}_{1}}{x}$＞k2x，则x的取值范围是（ ）
如图，反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A（-2，4），B两点，若$\frac{{k}_{1}}{x}$＞k2x，则x的取值范围是（ ）| A． | -2＜x＜0 | B． | -2＜x＜2 | C． | -2＜x＜0或x＞2 | D． | x＜-2或0＜x＜2 |
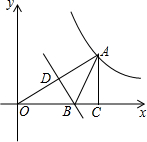如图，点A在双曲线y=$\frac{3}{x}$（x＞0）上，过点A作AC⊥x轴，垂足为C，线段OA的垂直平分线BD交x轴于点B，△ABC的周长为4，求点A的坐标．
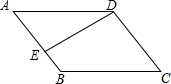如图，在?ABCD中，DE⊥AB于E，若∠C=70°，则∠ADE的大小为20度．
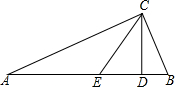如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，CE是△ABC的中线，∠BCD=22.5°．