题目内容
11.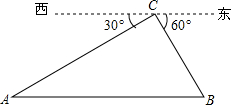 笔直的公路AB一侧有加油站C,已知从西面入口点A到C的距离为60米,西东两个入口A、B与加油站C之间的方向角如图所示,则A、B两个入口间的距离为( )
笔直的公路AB一侧有加油站C,已知从西面入口点A到C的距离为60米,西东两个入口A、B与加油站C之间的方向角如图所示,则A、B两个入口间的距离为( )| A. | 20$\sqrt{3}$米 | B. | 30$\sqrt{3}$米 | C. | 40$\sqrt{3}$米 | D. | 60$\sqrt{3}$米 |
分析 过C作CD⊥AB于D,根据平行线的性质求出∠CAD及∠CBD的度数,再根据特殊角的三角函数值解答即可.
解答 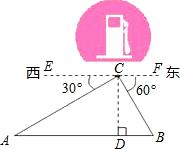 解:过C作CD⊥AB于D,∵EF∥AB,
解:过C作CD⊥AB于D,∵EF∥AB,
∴∠CAD=∠ACE=30°,∠ACF=∠CBD=60°,AC=60米,
∴CD=AC•sin∠ACE=60×$\frac{1}{2}$=30米,
由勾股定理得,AD=$\sqrt{6{0}^{2}-3{0}^{2}}$米;
在Rt△BCD中,∵∠CBD=60°,
∴BD=30tan30°=10$\sqrt{3}$米,
∴AB=AD+BD=40$\sqrt{3}$米.
故选:C.
点评 此题比较简单,解答此题的关键是作出辅助线,构造出直角三角形,利用平行线的性质及直角三角形的性质解答.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
2.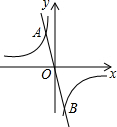 如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )
如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )
 如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )
如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )| A. | -2<x<0 | B. | -2<x<2 | C. | -2<x<0或x>2 | D. | x<-2或0<x<2 |
 如图,在?ABCD中,DE⊥AB于E,若∠C=70°,则∠ADE的大小为20度.
如图,在?ABCD中,DE⊥AB于E,若∠C=70°,则∠ADE的大小为20度.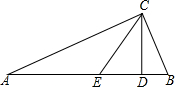 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CE是△ABC的中线,∠BCD=22.5°.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CE是△ABC的中线,∠BCD=22.5°.




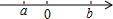 实数a,b在数轴上对应点的位置如图所示:则3a-$\sqrt{(3a-4b)^{2}}$=6a-4b.
实数a,b在数轴上对应点的位置如图所示:则3a-$\sqrt{(3a-4b)^{2}}$=6a-4b.