题目内容
 如图,在Rt△ABC中,∠C=90°,AM为△ABC 的角平分线,将线段BM绕点B顺时针方向旋转使点M刚好落在AM的延长线上的点N处,此时作ND⊥BC于点D.
如图,在Rt△ABC中,∠C=90°,AM为△ABC 的角平分线,将线段BM绕点B顺时针方向旋转使点M刚好落在AM的延长线上的点N处,此时作ND⊥BC于点D.(1)求证:∠ABN=90°;
(2)求证:CM=BD;
(3)若BD=
| 3 |
| 2 |
考点:旋转的性质,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)根据旋转的性质,可得对应线段相等,根据根据等腰三角形的性质,可得∠BMN与∠BNM的关系,根据相似三角形的判定与性质,可得答案;
(2)根据角平分线的性质,可得ME=CM,根据AAS,可得三角形全等,根据全等三角形的性质,可得答案;
(3)根据勾股定理,可得DN的长,根据等角的锐角三角函数相等,可得答案.
(2)根据角平分线的性质,可得ME=CM,根据AAS,可得三角形全等,根据全等三角形的性质,可得答案;
(3)根据勾股定理,可得DN的长,根据等角的锐角三角函数相等,可得答案.
解答:(1)证明:∵线段BM绕点B旋转后得线段BN
∴BM=BN
∴∠BMN=∠BNM,
∵AM平分∠BAC
∴∠CAM=∠BAM
∠AMC=∠BMN=∠BNM
∴△ACM∽△ABN
∴∠ABN=∠C=90°;
(2)证明:作ME⊥AB于E,
∵AM平分∠BAC,∠C=90°,ME⊥AB
∴ME=CM,
∵ND⊥BC于D
∴∠MEB=∠NDB=∠ABN=90°
∴∠MBE+∠MBN=∠MBN+∠BND=90°
∴∠MBE=∠BND
∵∠MEB=∠NDB,∠MBE=∠BND,BM=BN
∴△MEB≌△BDN(AAS),
∴ME=BD
∴CM=BD;
(3)解:设DM=2x,则CM=BD=3x,BN=BM=BD+DM=5x
在Rt△BDN中,DN=
=4x
在Rt△MDN中,tan∠MND=
=
=
,
∵∠C=∠NDM=90°
∴AC∥DN
∴∠BAM=∠CAM=∠MND,
∴tan∠BAM=tan∠MND=
在Rt△ABN中,BN=AB•tan∠BAM=10×
=5.
∴BM=BN
∴∠BMN=∠BNM,
∵AM平分∠BAC
∴∠CAM=∠BAM
∠AMC=∠BMN=∠BNM
∴△ACM∽△ABN
∴∠ABN=∠C=90°;
(2)证明:作ME⊥AB于E,

∵AM平分∠BAC,∠C=90°,ME⊥AB
∴ME=CM,
∵ND⊥BC于D
∴∠MEB=∠NDB=∠ABN=90°
∴∠MBE+∠MBN=∠MBN+∠BND=90°
∴∠MBE=∠BND
∵∠MEB=∠NDB,∠MBE=∠BND,BM=BN
∴△MEB≌△BDN(AAS),
∴ME=BD
∴CM=BD;
(3)解:设DM=2x,则CM=BD=3x,BN=BM=BD+DM=5x
在Rt△BDN中,DN=
| BN2-BD2 |
在Rt△MDN中,tan∠MND=
| DM |
| DN |
| 2x |
| 4x |
| 1 |
| 2 |
∵∠C=∠NDM=90°
∴AC∥DN
∴∠BAM=∠CAM=∠MND,
∴tan∠BAM=tan∠MND=
| 1 |
| 2 |
在Rt△ABN中,BN=AB•tan∠BAM=10×
| 1 |
| 2 |
点评:本题考查了旋转的性质,利用了旋转的性质,相似三角形的判定与性质,补角的性质,全等三角形的判定与性质,等角的锐角三角函数相等.

练习册系列答案
相关题目
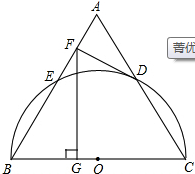 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.

 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则S四边形FEC'D'=
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则S四边形FEC'D'=