题目内容
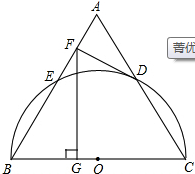 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.(1)求证:DF⊥AB;
(2)若AF的长为2,求FG的长.
考点:切线的性质,等边三角形的性质
专题:证明题
分析:(1)连结OD,根据切线的性质由DF是圆的切线得∠ODF=90°,再根据等边三角形的性质得∠C=∠A=∠B=60°,AB=AC,而OD=OC,所以∠ODC=60°=∠A,
于是可判断OD∥AB,根据平行线的性质得DF⊥AB;
(2)在Rt△ADF中,由∠A=60°得到∠ADF=30°,根据含30度的直角三角形三边的关系得AD=2AF=4,再证明OD为△ABC的中位线,则AD=CD=4,即AC=8,
所以AB=8,BF=AB-AF=6,然后在Rt△BFG中,根据正弦的定义计算FG的长.
于是可判断OD∥AB,根据平行线的性质得DF⊥AB;
(2)在Rt△ADF中,由∠A=60°得到∠ADF=30°,根据含30度的直角三角形三边的关系得AD=2AF=4,再证明OD为△ABC的中位线,则AD=CD=4,即AC=8,
所以AB=8,BF=AB-AF=6,然后在Rt△BFG中,根据正弦的定义计算FG的长.
解答:(1)证明: 连结OD,如图,
连结OD,如图,
∵DF是圆的切线,
∴OD⊥DF,
∴∠ODF=90°,
∵△ABC为等边三角形,
∴∠C=∠A=∠B=60°,AB=AC,
而OD=OC,
∴∠ODC=60°,
∴∠ODC=∠A,
∴OD∥AB,
∴DF⊥AB;
(2)解:在Rt△ADF中,∠A=60°,
∴∠ADF=30°,
∴AD=2AF=2×2=4,
而OD∥AB,点O为BC的中点,
∴OD为△ABC的中位线,
∴AD=CD=4,即AC=8,
∴AB=8,
∴BF=AB-AF=6,
∵FG⊥BC,
∴∠BGF=90°,
在Rt△BFG中,sinB=sin60°=
,
∴FG=6×
=3
.
 连结OD,如图,
连结OD,如图,∵DF是圆的切线,
∴OD⊥DF,
∴∠ODF=90°,
∵△ABC为等边三角形,
∴∠C=∠A=∠B=60°,AB=AC,
而OD=OC,
∴∠ODC=60°,
∴∠ODC=∠A,
∴OD∥AB,
∴DF⊥AB;
(2)解:在Rt△ADF中,∠A=60°,
∴∠ADF=30°,
∴AD=2AF=2×2=4,
而OD∥AB,点O为BC的中点,
∴OD为△ABC的中位线,
∴AD=CD=4,即AC=8,
∴AB=8,
∴BF=AB-AF=6,
∵FG⊥BC,
∴∠BGF=90°,
在Rt△BFG中,sinB=sin60°=
| FG |
| FB |
∴FG=6×
| ||
| 2 |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了等边三角形的性质.

练习册系列答案
相关题目
抛物线y=ax2+bx+c的图象向左平移2个单位,再向上平移1个单位后得抛物线y=-2x2,则原抛物线的解析式为( )
| A、y=-2(x+2)2-1 |
| B、y=-2(x+2)2+1 |
| C、y=-2(x+1)2+2 |
| D、y=-2(x-2)2-1 |
下列说法正确的是( )
| A、同号两数相加,其和比加数大 |
| B、异号两数相加,其和比两个加数都小 |
| C、两数相加,等于它们的绝对值相加 |
| D、两个正数相加和为正数,两个负数相加和为负数 |
用科学记数法表示0.0000907的结果正确的是( )
| A、9.1×10-4 |
| B、9.1×10-5 |
| C、9.0×10-5 |
| D、9.07×10-5 |
 如图,在Rt△ABC中,∠C=90°,AM为△ABC 的角平分线,将线段BM绕点B顺时针方向旋转使点M刚好落在AM的延长线上的点N处,此时作ND⊥BC于点D.
如图,在Rt△ABC中,∠C=90°,AM为△ABC 的角平分线,将线段BM绕点B顺时针方向旋转使点M刚好落在AM的延长线上的点N处,此时作ND⊥BC于点D.