题目内容
某外国语学校组织九年级学生参加数、科、英竞赛培训,下面两幅统计图反映了学生自愿报名(每人限报一科)的情况,请你根据图中信息回答下列问题:
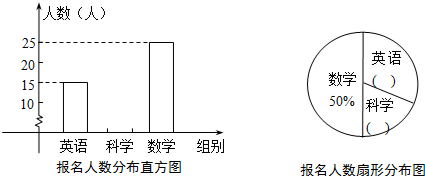
(1)九年级报名参加参加三科培训的总人数是 .
(2)英语学科所在扇形圆心角的度数是 ,请补全上述统计图.
(3)根据实际情况,需从英语组抽调部分同学到数学组,使数学组人数是英语组人数的3倍,则应从英语组抽调多少名学生?

(1)九年级报名参加参加三科培训的总人数是
(2)英语学科所在扇形圆心角的度数是
(3)根据实际情况,需从英语组抽调部分同学到数学组,使数学组人数是英语组人数的3倍,则应从英语组抽调多少名学生?
考点:频数(率)分布直方图,扇形统计图
专题:
分析:(1)根据参加化学培训的学生有25人,占总体的50%,即可计算出总人数;
(2)先用总人数减去参加数学与化学培训的人数,得出参加英语培训的人数,再除以总人数,得到参加数学培训的百分比,再乘以360°,得出所对应的圆心角的度数,然后补全统计图即可;
(3)设需从英语组抽调x名同学到数学组,根据数学组人数是英语组人数的3倍列方程求解.
(2)先用总人数减去参加数学与化学培训的人数,得出参加英语培训的人数,再除以总人数,得到参加数学培训的百分比,再乘以360°,得出所对应的圆心角的度数,然后补全统计图即可;
(3)设需从英语组抽调x名同学到数学组,根据数学组人数是英语组人数的3倍列方程求解.
解答:解:(1)∵参加数学培训的学生有25人,占总体的50%,
∴总人数为:25÷50%=50人.
故答案为50;
(2)∵参加科学培训的人数为:50-25-15=10人,
∴参加科学培训的百分比为:
×100%=20%,参加英语的百分比为:1-50%-20%=30%,
∴参加英语培训对应的圆心角为:360°×30%=108°;
如图:

(3)设需从英语组抽调x名同学到数学组,
根据题意得:3(15-x)=25+x,
解得x=5.
答:应从英语抽调5名学生到数学组.
∴总人数为:25÷50%=50人.
故答案为50;
(2)∵参加科学培训的人数为:50-25-15=10人,
∴参加科学培训的百分比为:
| 10 |
| 50 |
∴参加英语培训对应的圆心角为:360°×30%=108°;
如图:

(3)设需从英语组抽调x名同学到数学组,
根据题意得:3(15-x)=25+x,
解得x=5.
答:应从英语抽调5名学生到数学组.
点评:本题考查了扇形统计图及条形统计图的知识,难度一般,读懂统计图,能够从统计图中获得正确信息.

练习册系列答案
相关题目
抛物线y=ax2+bx+c的图象向左平移2个单位,再向上平移1个单位后得抛物线y=-2x2,则原抛物线的解析式为( )
| A、y=-2(x+2)2-1 |
| B、y=-2(x+2)2+1 |
| C、y=-2(x+1)2+2 |
| D、y=-2(x-2)2-1 |
 如图,在Rt△ABC中,∠C=90°,AM为△ABC 的角平分线,将线段BM绕点B顺时针方向旋转使点M刚好落在AM的延长线上的点N处,此时作ND⊥BC于点D.
如图,在Rt△ABC中,∠C=90°,AM为△ABC 的角平分线,将线段BM绕点B顺时针方向旋转使点M刚好落在AM的延长线上的点N处,此时作ND⊥BC于点D.