题目内容
3.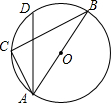 如图,△ABC内接于⊙O,AB为O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=3,则AC=$\sqrt{3}$.
如图,△ABC内接于⊙O,AB为O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=3,则AC=$\sqrt{3}$.
分析 连接BD,由圆周角定理和已知条件可求出AB的长,进而再直角三角形ACB中可求出AC的长.
解答 解:
连接BD,
∵AB为圆的直径,
∴∠C=∠D=90°,
∵∠CAB=60°,弦AD平分∠CAB,
∴∠DAB=30°,
∵AD=3,
∴AB=$\frac{AD}{cos30°}$=2$\sqrt{3}$,
∴AC=$\frac{1}{2}$AB=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 此题考查了三角形外接圆的有关性质以及圆周角定和特殊角的锐角三角函数值.此题难度适中,注意掌握直径所对的圆周角是直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理是解题关键.

练习册系列答案
相关题目
11.若点(x1,y1),(x2,y2)都是反比例函数y=-$\frac{1}{x}$图象上的点,并且y1<0<y2,则下列结论中正确的是( )
| A. | x1<x2 | B. | x2<x1 | ||
| C. | y随x的增大而增大 | D. | 两点有可能在同一象限 |
18.下列四个实数最小的是( )
| A. | -1 | B. | -$\sqrt{2}$ | C. | 0 | D. | 1 |
8.若x1,x2是一元二次方程x2+ax-8=0的两个根,则x1•x2的值是( )
| A. | a | B. | -a | C. | 8 | D. | -8 |
12.一枚质地均匀的六面骰子,六个面上分别刻有1,2,3,4,5,6点,投掷一次得到的点数为奇数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
 已知:O是坐标原点,P(m,n)(m>0)是函数y=$\frac{k}{x}$(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+$\frac{{n}^{4}}{4}$.
已知:O是坐标原点,P(m,n)(m>0)是函数y=$\frac{k}{x}$(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+$\frac{{n}^{4}}{4}$. 如图是由5个相同的正方体组成的一个立体图形,它的左视图是( )
如图是由5个相同的正方体组成的一个立体图形,它的左视图是( )



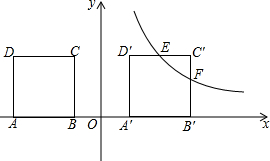 如图,在平面直角坐标系中,正方形ABCD顶点D(-3,2),B(1,0),CD∥x轴,将正方形ABCD向右平移m个单位,得正方形A′B′C′D′.当 m=4时,反比例函数y=$\frac{k}{x}$(x>0)的图象过线段C′D′的中点E,与线段B′C′交于点F.
如图,在平面直角坐标系中,正方形ABCD顶点D(-3,2),B(1,0),CD∥x轴,将正方形ABCD向右平移m个单位,得正方形A′B′C′D′.当 m=4时,反比例函数y=$\frac{k}{x}$(x>0)的图象过线段C′D′的中点E,与线段B′C′交于点F.