题目内容
先分解因式,再求解:
(1)已知x+y=1,xy=-
,求x(x+y)(x-y)-x(x+y)2的值.
(2)a2+a3+
a,其中a=-0.5;
(3)x2+xy-5x-5,其中x=6,y=-
.
(1)已知x+y=1,xy=-
| 1 |
| 2 |
(2)a2+a3+
| 1 |
| 4 |
(3)x2+xy-5x-5,其中x=6,y=-
| 1 |
| 6 |
考点:因式分解的应用
专题:
分析:(1)先利用提取公因式法因式分解,再进一步整体代入求得答案即可;
(2)先提取公因式,再进一步利用完全平方公式因式分解,最后代入求得数值即可;
(3)直接代入求得答案即可.
(2)先提取公因式,再进一步利用完全平方公式因式分解,最后代入求得数值即可;
(3)直接代入求得答案即可.
解答:解:(1)x(x+y)(x-y)-x(x+y)2
=x(x+y)(x-y-x-y)
=-2xy(x+y)
把x+y=1,xy=-
,代入得
原式=1.
(2)原式=a(a2+a+
)
=a(a+
)2
当a=-0.5时,
原式=0.
(3)当x=6,y=-
时,
原式=62+6×(-
)-5×6-5=0.
=x(x+y)(x-y-x-y)
=-2xy(x+y)
把x+y=1,xy=-
| 1 |
| 2 |
原式=1.
(2)原式=a(a2+a+
| 1 |
| 4 |
=a(a+
| 1 |
| 2 |
当a=-0.5时,
原式=0.
(3)当x=6,y=-
| 1 |
| 6 |
原式=62+6×(-
| 1 |
| 6 |
点评:此题考查因式分解的运用与整式的化简求值,注意整体代入思想的渗透.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 已知线段AB,阅读下列语句,分别画出相应的图形.
已知线段AB,阅读下列语句,分别画出相应的图形. 从楼房顶向下看,如图.一个为直角的墙角,直角边4米,一根长为5米的绳,一端拴在直角顶点处,另一端系着一只小羊P,小羊能活动到的最大面积是
从楼房顶向下看,如图.一个为直角的墙角,直角边4米,一根长为5米的绳,一端拴在直角顶点处,另一端系着一只小羊P,小羊能活动到的最大面积是 如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为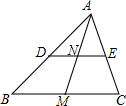 如图,△ABC中,AM是中线,点D、E分别在边AB、AC上,连接DE,且DE∥BC交AM于N,若DN=3,则DE=
如图,△ABC中,AM是中线,点D、E分别在边AB、AC上,连接DE,且DE∥BC交AM于N,若DN=3,则DE=