题目内容
在菱形ABCD中,已知AC=
,BD=
,那么菱形ABCD的边长为 ,面积为 .
| 8 |
| 12 |
考点:菱形的性质
专题:
分析:根据菱形的对角线互相垂直平分及勾股定理即可求得其边长利用菱形的面积=两对角线乘积的一半可以求出菱形ABCD的面积.
解答: 解:如图,∵AC=
解:如图,∵AC=
=2
,BD=
=2
,
∴AO=
,BO=
,
∵AC⊥BD,
∴AB=
=
,
即菱形ABCD的边长为
,
根据菱形的面积=两对角线乘积的一半可得:
菱形ABCD的面积=
×2
×2
=2
,
故答案为
,2
.
 解:如图,∵AC=
解:如图,∵AC=| 8 |
| 2 |
| 12 |
| 3 |
∴AO=
| 2 |
| 3 |
∵AC⊥BD,
∴AB=
| 2+3 |
| 5 |
即菱形ABCD的边长为
| 5 |
根据菱形的面积=两对角线乘积的一半可得:
菱形ABCD的面积=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
故答案为
| 5 |
| 6 |
点评:此题主要考查菱形的基本性质:菱形的对角线互相垂直平分,以及勾股定理的运用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
下列函数中.y是x的反比例函数的是( )
A、y=
| ||||
B、y=-
| ||||
C、y=
| ||||
D、y=1-
|
以下说法中正确的是( )
| A、符号不同的数互为相反数 |
| B、除以一个数等于乘于这个数的倒数 |
| C、规定了原点、正方向和单位长度的直线叫做数轴 |
| D、一个数的绝对值越大,表示它的点在数轴上越靠右 |
当k•b<0时,一次函数y=kx-b的图象大致是( )
A、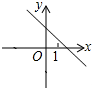 |
B、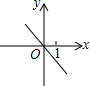 |
C、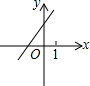 |
D、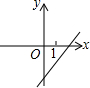 |
 已知△ABC,A(-3,2),B(-2,-1),C(2,3),利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的△A1B1C1.
已知△ABC,A(-3,2),B(-2,-1),C(2,3),利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的△A1B1C1. 如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,∠D=∠AOD,若∠BAC=80°,则∠BCA的度数为 如图,已知△ABC中,BD平分∠ABC,CE=CD,DB=DE,∠E=30°.
如图,已知△ABC中,BD平分∠ABC,CE=CD,DB=DE,∠E=30°.