题目内容
16.不等式组$\left\{\begin{array}{l}{2(x+3)>5(x-1)}\\{\frac{1-x}{2}<\frac{x+2}{3}+1}\end{array}\right.$的整数解为-1、0、1、2、3.分析 先分别求出各不等式的解集,再求出其公共解集,再其公共解集内找出符合条件的x的所有整数解即可.
解答 解:解不等式2(x+3)>5(x-1),得:x<$\frac{11}{3}$,
解不等式$\frac{x-1}{2}$<$\frac{x+2}{3}$+1,得:x>-$\frac{7}{5}$,
∴不等式组的解集为:-$\frac{7}{5}$<x<$\frac{11}{3}$,
符合条件的x的整数解为:-1、0、1、2、3,
故答案为:-1、0、1、2、3.
点评 本题考查的是解一元一次不等式组及求一元一次不等式组的整数解,求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

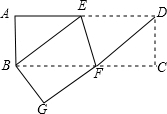 如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE.
如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE. 如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7.
如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7. 如图,已知一次函数y=kx+b的图象与x轴交于点A(5,0),与函数y=2x的图象交于点M,点M的横坐标为2,求点M的坐标及函数y=kx+b的表达式.
如图,已知一次函数y=kx+b的图象与x轴交于点A(5,0),与函数y=2x的图象交于点M,点M的横坐标为2,求点M的坐标及函数y=kx+b的表达式.