题目内容
6.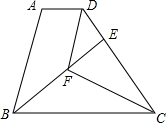 已知,如图,在梯形ABCD中,AD∥BC,BC=CD,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.
已知,如图,在梯形ABCD中,AD∥BC,BC=CD,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.(1)△BFC与△DFC全等吗?试说明你的理由.
(2)AD与DE相等吗?试说明你的理由.
分析 (1)由CF平分∠BCD可知∠BCF=∠DCF,然后通过SAS就能证出△BFC≌△DFC.
(2)要证明AD=DE,连接BD,证明△BAD≌△BED则可.根据AB∥DF,推出∠ABD=∠BDF,由于BF=DF,于是得到∠DBF=∠BDF,等量代换得到∠ABD=∠EBD,根据等腰三角形的性质得到BD=BD,即可得到∠BDA=∠DBC=∠BDC,于是得到结论.
解答 证明:(1)∵CF平分∠BCD,
∴∠BCF=∠DCF.
在△BFC和△DFC中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCF=∠DCF}\\{FC=FC}\end{array}\right.$,
∴△BFC≌△DFC(SAS).
(2)连接BD.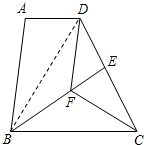
∵△BFC≌△DFC,
∴BF=DF,
∴∠FBD=∠FDB.
∵DF∥AB,
∴∠ABD=∠FDB.
∴∠ABD=∠FBD.
∵AD∥BC,
∴∠BDA=∠DBC.
∵BC=DC,
∴∠DBC=∠BDC.
∴∠BDA=∠BDC.
在△BAD与△BED中,
$\left\{\begin{array}{l}{∠ABD=∠FBD}\\{BD=BD}\\{∠ADB=BDC}\end{array}\right.$,
∴△BAD≌△BED(ASA),
∴AD=DE.
点评 此题考查了梯形的性质、平行四边形的判定与性质以及全等三角形的判定与性质.此题难度适中,解题的关键是准确作出辅助线,利用数形结合的思想求解.

练习册系列答案
相关题目
16. 如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )
如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )
(1)$\frac{BP}{AP}=\frac{AP}{AB}$;(2)AB:AP=AP:PB;(3)BP2=AP•AB;(4)$\frac{AP}{AB}$≈0.618.
 如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )
如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )(1)$\frac{BP}{AP}=\frac{AP}{AB}$;(2)AB:AP=AP:PB;(3)BP2=AP•AB;(4)$\frac{AP}{AB}$≈0.618.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.在有理数范围内,不论x为何值,x2+x+1的值永远是( )
| A. | 正数 | B. | 非负数 | C. | 负数 | D. | 不确定 |
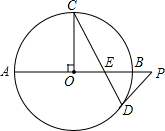 如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.
如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.