题目内容
15.在有理数范围内,不论x为何值,x2+x+1的值永远是( )| A. | 正数 | B. | 非负数 | C. | 负数 | D. | 不确定 |
分析 原式配方后,利用非负数的性质判断即可.
解答 解:x2+x+1=x2+x+$\frac{1}{4}$-$\frac{1}{4}$=(x+$\frac{1}{2}$)2-$\frac{1}{4}$≥-$\frac{1}{4}$,
则在有理数范围内,不论x为何值,x2+x+1的值永远是不确定,
故选D
点评 此题考查了配方法的应用,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.一次函数y=3x-4的截距是( )
| A. | 4 | B. | -4 | C. | 3 | D. | -3 |
7.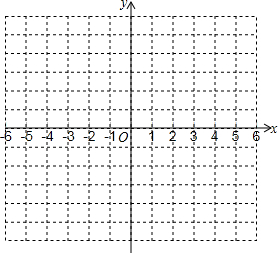 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,
(1)用配方法把化为y=a(x+m)2+k的形式;
(2)选取适当的数据填入表,并在所给的直角坐标系内描点画出该抛物线的图象;
(3)若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,根据图象可知y1<y2.(填“<”或“>”)
 已知二次函数y=-x2+2x+2,
已知二次函数y=-x2+2x+2,(1)用配方法把化为y=a(x+m)2+k的形式;
(2)选取适当的数据填入表,并在所给的直角坐标系内描点画出该抛物线的图象;
| x | … | … | |||||
| y | … | … |
5.一元二次方程x2-2x+3=0的根的情况是( )
| A. | 有两个相等的实根 | B. | 有两个不相等的实根 | ||
| C. | 无实数根 | D. | 有一个根 |
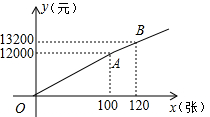 获取信息:某市体育馆将举办明星篮球赛,为此体育馆推出两种团体购票方案(设购票张数为x张,购票总价为y元):
获取信息:某市体育馆将举办明星篮球赛,为此体育馆推出两种团体购票方案(设购票张数为x张,购票总价为y元):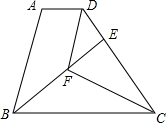 已知,如图,在梯形ABCD中,AD∥BC,BC=CD,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.
已知,如图,在梯形ABCD中,AD∥BC,BC=CD,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.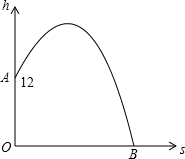 家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米.
家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米.