题目内容
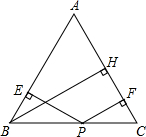 如图,已知等边三角形ABC中,P为底边BC上任意一点,PE⊥AB于E,PF⊥AC于F,BH⊥AC于H,求证:PE+PF=BH.
如图,已知等边三角形ABC中,P为底边BC上任意一点,PE⊥AB于E,PF⊥AC于F,BH⊥AC于H,求证:PE+PF=BH.考点:等边三角形的性质
专题:证明题
分析:连接AP,可分别表示出△ABC、△ABP、△ACP的面积,根据面积相等可证得结论.
解答: 证明:
证明:
连接AP,
∵PE⊥AB,PF⊥AC,BH⊥AC,
∴S△ABP=
AB•PE,S△ACP=
AC•PF,S△ABC=
AC•BH,
∵S△ABP+S△ACP=S△ABC,
∴
AB•PE+
AC•PF=
AC•BH,
∴AB•PE+AC•PF=AC•BH,
∵△ABC为等边三角形,
∴AB=AC,
∴PE+PF=BH.
 证明:
证明:连接AP,
∵PE⊥AB,PF⊥AC,BH⊥AC,
∴S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABP+S△ACP=S△ABC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AB•PE+AC•PF=AC•BH,
∵△ABC为等边三角形,
∴AB=AC,
∴PE+PF=BH.
点评:本题主要考查等边三角形的性质及等积法,利用等积法得到AB•PE+AC•PF=AC•BH是解题的关键.

练习册系列答案
相关题目
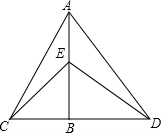 如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,下列说法中:①△ABC≌△DBE;②△ACB≌△ABD;③△CBE≌△BED;④△ACE≌△ADE.正确的是( )
如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,下列说法中:①△ABC≌△DBE;②△ACB≌△ABD;③△CBE≌△BED;④△ACE≌△ADE.正确的是( )| A、①②③ | B、① |
| C、①③④ | D、②③④ |
 如图,在数轴上表示的解集用不等式表示为( )
如图,在数轴上表示的解集用不等式表示为( )| A、2<x<4 |
| B、-2<x≤4 |
| C、-2≤x<4 |
| D、-2≤x≤4 |
 如图是由4个边长为1的正方形组成的图形,请求出∠ABC的度数.
如图是由4个边长为1的正方形组成的图形,请求出∠ABC的度数. 已知,如图,O是四边形ABCD内一点,且∠OBC=
已知,如图,O是四边形ABCD内一点,且∠OBC=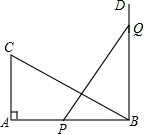 如图,Rt△ABC中,∠A=90°,AC=6,AB=8,BD⊥AB,P,Q分别为AB,BD上的动点且PQ=BC,点P在AB上的什么位置时,△PQB与△ABC全等?
如图,Rt△ABC中,∠A=90°,AC=6,AB=8,BD⊥AB,P,Q分别为AB,BD上的动点且PQ=BC,点P在AB上的什么位置时,△PQB与△ABC全等?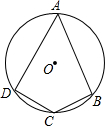 如图,四边形ABCD的四个顶点都在圆上,称这样的四边形为圆内接四边形.这个圆称为四边形的外接圆.下面证明定理:圆内接四边形的对角互补.
如图,四边形ABCD的四个顶点都在圆上,称这样的四边形为圆内接四边形.这个圆称为四边形的外接圆.下面证明定理:圆内接四边形的对角互补.