题目内容
20.在一个不透明的盒子里,装有三个分别写有数字6,2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树状图或列表的方法,求下列事件的概率:(1)两次取出小球上的数字相同;
(2)两次取出小球上的数字之和大于10.
分析 (1)画树形图展示所有9种等可能的结果数,再找出两次取出小球上的数字相同的结果数,然后根据概率公式求解;
(2)从树状图中找出两次取出小球上的数字之和大于10的结果数,然后根据概率公式求解.
解答 解:(1)画树形图为:
共有9种等可能的结果数,其中两次取出小球上的数字相同的结果数为3,
所以两次取出小球上的数字相同的概率=$\frac{3}{9}$=$\frac{1}{3}$;
(2)两次取出小球上的数字之和大于10的结果数为4,
所以两次取出小球上的数字之和大于10的概率=$\frac{4}{9}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15.把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,则锐角A、A′的余弦值之间的关系为( )
| A. | cos A=cos A′ | B. | cos A=3cos A′ | C. | 3 cos A=cos A′ | D. | 不能确定 |
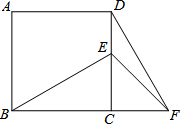 如图,在正方形ABCD中,E为CD边上的一点,F为BC延长线上一点,CE=CF,∠FDC=30°,则∠BEF的度数为105°.
如图,在正方形ABCD中,E为CD边上的一点,F为BC延长线上一点,CE=CF,∠FDC=30°,则∠BEF的度数为105°. 如图是证明勾股定理的一种方法:用4个全等的直角三角形,拼成一个图形,请你利用面积证明勾股定理的真实性.
如图是证明勾股定理的一种方法:用4个全等的直角三角形,拼成一个图形,请你利用面积证明勾股定理的真实性.