题目内容
16. 在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线交AB于点E,交BC于点D,连接AD,CD=3cm,则BD的长为6cm.
在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线交AB于点E,交BC于点D,连接AD,CD=3cm,则BD的长为6cm.
分析 利用垂直平分线的性质可得∠DAE=∠B=30°,可得∠DAC=30°,易得AD=BD=2CD,可得BD.
解答 解:∵在△ABC中,∠C=90°,∠B=30°,
∴∠BAC=60°,
∵DE为AB的垂直平分线,
∴AD=BD,
∴∠DAE=∠B=30°,
∴∠CAD=30°,
∴CD=$\frac{1}{2}AD=\frac{1}{2}BD$,
∴BD=2CD=2×3=6,
故答案为:6.
点评 本题主要考查了垂直平分线的性质和含30°直角三角形的性质,综合运用各性质定理是解答此题的关键.

练习册系列答案
相关题目
1.(-2m-1)2=( )
| A. | 4m2+1 | B. | 4m2-1 | C. | 4m2+4m+1 | D. | 4m2-4m+1 |
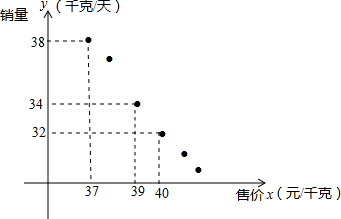 某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.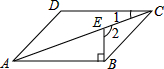 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为110°.
如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为110°. 如图,图中所有的三角形都是直角三角形,四边形都是正方形,其中最大正方形E的边长为10,则四个正方形A,B,C,D的面积之和为100.
如图,图中所有的三角形都是直角三角形,四边形都是正方形,其中最大正方形E的边长为10,则四个正方形A,B,C,D的面积之和为100.